Публикации FreePascal

FreePascal и длинные числа. Часть 1. Библиотека GNU Multiple Precision Arithmetic (GMP)

11.04.2019
Вадим Исаев

Учитывая текущее плачевное состояние наших программ, можно сказать, что программирование – определённо всё ещё чёрная магия и пока мы не можем называть её технической дисциплиной.

Билл Клинтон, бывший президент США

Аннотация
Небольшое предисловие
Краткое описание библиотеки GMP
Предварительная подготовка
Арифметика GMP. Краткий курс
1. Создание и удаление переменных
2. Присвоение переменным значений
3. Вывод переменных на экран
4. Арифметические операции
5. Сравнительные операции
6. Диагностика и выуживание стандартных типов
7. Немного практики
Скорость работы GMP
Сборка библиотеки GMP вручную
Как сделать gmp.pas посовременнее
Заключение
Ссылки

1. Аннотация

Цикл статей в трёх частях с прологом и эпилогом, в которых описывается использование стандартных для Linux (в Windows ставятся как сторонние) библиотек, позволяющих работать с длинными числами, у которых длина мантиссы выходит за пределы возможностей стандартных типов данных. В части 1 (текущей) кратко описывается работа FreePascal с базовой библиотекой GNU Multiple Precision Arithmetic (GMP)[1]. Часть 2 посвящена библиотеке MPFR и третья часть - библиотеке MPC.

Статьи будут интересны тем, кто использует FreePascal в вычислительных проектах.

2. Небольшое предисловие

Ни для кого не секрет, что для решения большинства уравнений современной науки и техники требуются типы данных для представления десятичных дробей и, чаще всего, чисел с плавающей точкой. Хотя я разделяю всеобщее повальное заблуждение о том, что большинство задач можно решить используя типы 8-мибайтовой длины (типа "Double" в Pascal\C\C++ и "Real(8)" в Fortran), у которых длина мантиссы равна 16-ти разрядам, но ведь не исключена вероятность, что этих 16-ти разрядов может и не хватить.

Некоторые особо романтические программисты если им не хватает размеров типа "Double" легко меняют его на тип "Extended" и думают, что дела от этого сразу поправятся. Как бы ни так! Тип "Extended" - довольно подозрительная штука, что очень легко проиллюстрировать. Вот простой пример:

program primer1;

Var
  e: extended;
  d: double;

Begin
  e:=1.2;
  d:=1.2;
  WriteLn('Тип Extended. Должно быть: 1.2; На самом деле: ', e);
  WriteLn('Тип Double.   Должно быть: 1.2; На самом деле: ', d);
End.

Рисунок 1. У типа "Extended" появился хвост

Интересно, не правда ли? У типа "Extended" в результате самого обычного присваивания появился хвост. Если вы решите его игнорировать, потому что он явно лежит вне пределов значимых разрядов числа, то сделаете это зря - присвоение разных чисел даёт для типа "Extended" хвосты разной длины. И длина хвоста сильно зависит от размера экспоненты. Мало того, иногда хвост даже будет портить исходные данные:

program primer2;

Var
  e: extended;
  d: double;

Begin
  e:=3.1415e1888;
  WriteLn('Тип Extended. Должно быть 3.1415 E+1888, На самом деле: ', e);
  d:=3.1415e307;
  WriteLn('Тип Double.   Должно быть 3.1415 E+307,  На самом деле: ', d);
End.

Рисунок 2. У типа "Extended" хвост виляет собакой

Ну и как вам это нравится? Хвост у "Extended" не просто стал длинным, а ещё и испортил само число, значимые разряды. Судя по рис. 2, единственное достоинство типа "Extended" - большая чем у типа "Double" величина экспоненты - на деле оказывается весьма сомнительным. И я сильно подозреваю, что эта величина паразитирует на мантиссе.

В примерах специально добавлен тип "Double" чтобы показать, что подобный хвост есть только у "Extended". Интересные дела творятся на белом свете. И это даже не принимая во внимание, что типы с плавающей точкой сами по себе не точные из-за округления младшего разряда. Кроме округленческой ошибки, со стандартными типами данных можно запросто наловить и другие ошибки, некоторые из них описаны в [12].

Что-же делать, неужели точные вычисления с большими числами совершенно недоступны? Не стоит так уж сильно горевать. В принципе, для работы с длинными числами можно накалякать и собственный модуль, у которого длина мантиссы - величина динамическая. А длинные числа положительно повлияют и на точность, даже с учётом округления, если в округлении возникнет надобность. Идея витает в воздухе - создать массив целых чисел, где каждая ячейка массива - один разряд числа. Как сделать плюс-минус-разделить-умножить в столбик надеюсь никто не забыл. Возведение в степень - через операцию умножения. Извлечение корня - через операцию возведения в степень. И так далее, делая более сложные операции на основе всё тех же арифметических. Вот только тратить на это время не особо хочется... А собственно и не надо, потому что подобные библиотеки давно уже существуют. Для UNIX систем это стандартный комплект библиотек который, если уже не установлен в вашей системе по умолчанию, можно запросто установить из репозитория. Несчастным владельцам Windows придётся повозиться чуть-чуть подольше - например, поставить себе CYGWIN или MINGW, в которых эти библиотеки сделаны для Windows.

На рис. 3 представлена иерархия библиотек для работы с длинными числами:

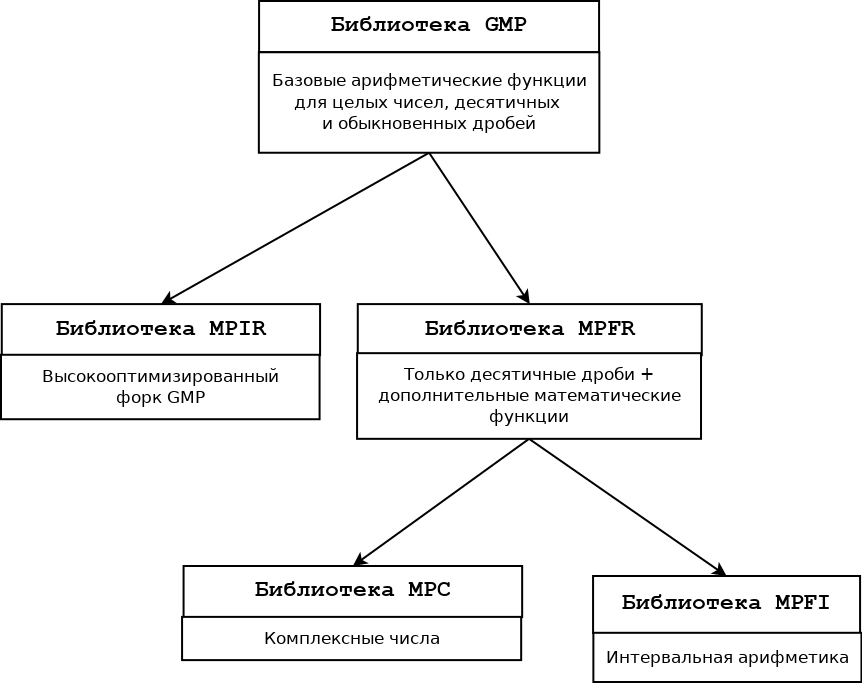
Рисунок 3. Система библиотек для работы с длинными числами

Длинные числа начинаются с библиотеки GMP, в которой реализованы базовые типы длинных чисел и базовые арифметические и логические операции над ними. На её основе сделана библиотека MPFR, в которую из GMP перекочевала только часть по работе с десятичными дробями или, говоря по научному - числа с плавающей или фиксированной точкой. Туда же добавлено большое количество дополнительных функций, например тригонометрических. В отличие от GMP, в MPFR для любой аривметической операции или функции требуется задать правило округления, согласно IEEE754. На основе MPFR сделана бибилиотека MPC, в которой реализована работа с комплексными числами и библиотека MPFI, которая работает не с отдельными числами, а с интервалами, т.е. задаётся минимальное и максимальное число, представляющие собой интервал в пределах которого лежит ответ.

Особо нужно сказать про библиотеку MPIR. Её имеет смысл использовать при самостоятельной сборке на своём компьютере. Скрипт "configure", который делает "Makefile", определяет тип вашего процессора и вводит в "Makefile" соответствующие ключи оптимизации для увеличения скорости работы именно с этим процессором. А по своему функционалу она идентична библиотеке GMP.

В FreePascal, начиная по-моему с версии 2.6, есть модуль "gmp.pas", который позволяет пользоваться библиотекой GMP в программах на языке Паскаль, чтобы не заморачиваться изобретением собственного модуля длинных чисел или не тратить время на поиски такового в Интернет.

3. Краткое описание библиотеки GMP

Главное, что в ней греет душу - библиотека бесплатная. Может работать:

с целыми числами;
с десятичными дробями;
с обыкновенными дробями. Это является интересным сюрпризом, поскольку я сильно подозреваю, что нынешнее поколение, которое прямо с зачатия привыкло к современным компьютерам, уже видимо даже изобразить их не сможет, не говоря уж о том, чтобы провести с ними какие-нибудь арифметические действия.

Небольшое лирическое отступление по поводу обыкновенных дробей
Чтобы вы не думали, что в последнем пункте я применяю тут к вам шутки юмора, давайте сразу же протестируемся. Решите в уме следующую несложную задачку:
4 − 2 : ½ + 1

Ответ, вместе с условием задачи естественно, можно отослать ректору того ВУЗа, где вам выдали диплом. Для справки: 60 % выпускников университетов США правильно решить эту задачу без компьютера не могут.

В оригинале библиотеки длинные числа представлены в двух видах и двух отдельно лежащих заголовочных файлах:

В, так сказать, низкоуровневом (сишном) виде. Эти типы применяются в языке Си. При этом арифметические операции с числами можно проводить только с помощью специальных функций. Однако в FreePascal, в отличие от Си, для этих типов можно сомостоятельно переопределить арифметические операции, как это сделано для следующего вида;
В высокоуровневом (си-плюсплюснутом) виде, где числа представлены в виде классов\интерфейсов. Этот вид изначально предназначался только для Си++. Текст программы с ними выглядит намного короче и понятнее, т.к. с такими типами чисел можно применять обычные знаки арифметических операций.

У FreePascal нет разделения на язык с классами и язык без классов, поэтому заголовочный файл, который идёт в комплекте FCL, для обоих видов один и в программах можно применять любое из двух представлений, на ваш выбор.

Сишные числовые типы в библиотеке представлены в сложносоставном формате - в виде записи (в Си - структуры) с набором полей:

Для целого числа тип называется "mpz_t". Состоит из полей:
- alloc - здесь хранится количество неких "попугаев" (на ихнем языке - "лимбов"), которые выделены для хранения числа. Тип данных - longint;
- size - здесь хранится сколько конкретно "лимбов" занято реальным числом. Причём если значение со знаком "-", то само число является отрицательным. Тип данных - longint;
- data - ну а это и так понятно, указатель для данных под число.
Сколько в одном "попугае" ("лимбе") содержится битов можно узнать с помощью функции "bits_per_limb()". В 64-разрядных ОС (и, конечно же, с применением 64-разрядных компиляторов) в одном "попугае\лимбе" содержится 64 бита, а в 32-разрядных - ожидаемо 32.
По косвенным данным, количество "попугаев" в переменной целого типа может автоматически добавляться, если заранее выделенного места не хватило под вводимое в этот тип число. По крайней мере эксперименты показали, что если при инициализации переменной указать ему некое значение "попугаев", а потом в эту переменную ввести число явно превышающее по размерам ранее выделенное место, то программа не ругается, а просто заново выделяет необходимую память и число, таким образом, не искажается.
Для десятичных дробей (с фиксированной или плавающей точкой) тип называется "mpf_t". Состоит из полей:
- prec - сколько "попугаев" ("лимбов") отведено под мантиссу. Тип данных - longint;
- size - тоже, что и для предыдущего типа. Тип данных - longint;
- exp - сколько "попугаев" отведено под экспоненту. Тип данных:
  - для 64-битного компилятора - int64,
  - для 32-битного - longint;
- data - указатель на данные.
  В отличие от предыдущего типа, здесь автоматического добавления памяти при нехватке места под число (экспоненту) почему-то не предусмотрено. Т.е. введя число по количеству разрядов в мантиссе превышающее ранее выделенную память, мы в дальнейшем будем манипулировать обрезанным числом. Правда некоторый запас по увеличению количества разрядов всё же будет, т.к. память под числа выделяется в размере кратном "лимбу", с округлением до ближайщего большего целого. Однако работая с этим типом данных необходимо тщательно следить, хватит ли выделенной для переменной памяти. Точнее говоря, тщательно и скурпулёзно проводить проектирование программы на предмет максимально возможного количества разрядов в мантиссе. Самое печальное здесь - если памяти не хватает, то программа ни гу-гу об этом, как будто так и надо...
  В отличие от мантиссы, память под экспоненту ничем заранее не определяется. Почему так происходит будет объяснено несколько ниже, там где рассказывается про форму вывода числа на экран. По умолчанию при инициализации экспонента вообще не предусмотрена, что можно проверить посмотрев значение поля "exp". Однако для неё в поле "prec" добавляется один дополнительный "лимб". После присвоения переменной какого-нибудь значения, поле экспоненты тут же заполняется "лимбами". Правда верить этому значению нельзя. Эксперименты показали, что если в переменную поместить десятичную дробь вообще без экспоненты, (что-то типа "7.62"), то под экспоненту всё равно автоматом выделяется один лимб. Если же экспонента явно присутствует (что-то типа "2.99792458e08"), то количество лимбов под экспоненту может приобретать совершенно фантастические размеры.
Для обыкновенной дроби тип называется "mpq_t". Состоит из полей:
- num, типа "mpz_t" - числитель или по английски "numerator";
- den, типа "mpz_t" - знаменатель или по английски "denominator ".

Си-плюсплюснутые типы позволяют применять объектно-ориентированный подход и, в ряде случаев, сделать вид программного кода более простым и читабельным. В "gmp.pas" присутствуют как интерфейсы, так и классы, которые сделаны на базе этих интерфейсов. Стоит ли использовать именно класс - на ваше усмотрение. По моему мнению интерфейс гораздо удобнее в применении, потому что при этом класс всё равно создаётся, но автоматически, без участия программиста. MPInteger (интерфейс), TMPInteger (класс) - для целых чисел; MPFloat (интерфейс), TMPFloat (класс) - для десятичных дробей; MPRational (интерфейс), TMPRational (класс) - для обыкновенных дробей.

Внутри каждого интерфейса есть функция (а внутри классов - функция и скрытое поле), представляющие соответствующий сишный тип данных. К сожалению у этого удобного для программиста вида типов есть и большой минус - программы на их основе тратят времени на вычисления куда больше, чем при использовании низкоуровневых типов.

Над числом каждого типа можно производить арифметические операции, присваивать значения, извлекать корни, возводить в степень, сравнивать и преобразовывать в некоторые элементарные типы, например в строку, чтобы вывести на экран или в файл. Низкоуровневые типы необходимо перед применением инициализировать, а после использования - утилизировать.

Теоретические пределы обрабатываемых с помощью GMP чисел
Конечно же всё зависит от того, сколько у нас оперативной памяти и насколько она забита другими программами. Именно оперативной, поскольку своп-память на три порядка ухудшит время расчётов. На миг зажмуримся и представим, что памяти у нас сколько угодно. В таком случае:

Для целых чисел мантисса может составлять:

для 32 разрядов: 20,5 миллиардов разрядов
для 64 разрядов: 413 триллионов разрядов

Для десятичных дробей мантисса аналогичная, а вот экспонента:

для 32 разрядов: 20,5 миллиардов разрядов;
для 64 разрядов: 1,7E+20 разрядов.

Если найдётся герой способный изобразить такие бешеные цифры - добро пожаловать в нобилевский комитет за премией... Сами разработчики скромно указывают диапазон для 32-битной системы более чем от 2^-68719476768 до 2^68719476736.

4. Предварительная подготовка

Библиотеку сначала нужно установить в вашу систему. Если у вас Linux\*BSD, то скорее всего она уже установлена по умолчанию. Если же это не так, то её можно установить через репозиторий вашей операционной системы. В самом простейшем случае вам нужны только "libgmp" и "libgmp-devel" (или "libgmp-dev"). Версии пакета для разработчиков нужны именно FreePascal, т.к. он ищет названия библиотек, которые заканчиваются на ".so", а разработческие версии как раз делают такие симлинки. Но можно и самому ручками сделать симлинк, и для этого нужны права "root".

С Windows не всё так просто. К примеру, на моём рабочем компьютере с Windows уже стояла система CYGWIN в которой, судя по сообщению инсталлятора, "libgmp" была установлена по умолчанию. Ну, хорошо, компилирую примеры - всё прекрасно компилируется. Запускаю и, ёлки зелёные, получаю системное окошко с сообщением, что у меня отсутствует "gmp.dll". После некоторых размышлений и поисков выяснилось, что "libgmp" всё-таки стоит, вот только называется она почему-то "cyggmp-10.dll". Ну, ладно, сделал я ей новое имя, то которе положено - "libgmp.dll". Запускаю тестовую программу, ошибок больше не появляется, зато, программа зависла и не работает. Мало того, с помощью "Ctrl-C" завершить её невозможно, пришлось лезть в диспетчер задач.

Плюнув на CYGWIN я решил разжиться библиотекой в MINGW [2]. Имя у неё оказалось вполне нормальным, хотя и не каноническим - "libgmp-10.dll", так что опять пришлось переименовывать. Слегка мандражируя, снова запускаю тестовый пример и - свершилось чудо - пример отработал так, как нужно. Значит библиотеку 'libgmp" от MINGW можно без большого количества телодвижений спокойно использовать в Windows.

5. Арифметика GMP. Краткий курс

Поскольку функций в GMP много, но они различаются только префиксами и типами передаваемых туда праметров, для описания буду применять такой шаблон: префикс_ОсновноеНазваниеФункции(параметр1[, параметр2, ... ])

Для сишных типов все операции-функций имеют префикс соответствующий тому или иному типу:

"mpz" - для обработки целочисленных типов. Параметры туда передаются (в основном) типа "mpz_t";
"mpf" - для обработки типов с плавающей точкой. Параметры туда передаются (в основном) типа "mpf_t";
"mpq" - для обработки типов обыкновенных дробей. Параметры туда передаются (в основном) типа "mpq_t"

Для функций, которые применяются к переменной того или иного класса-интерфейса, префиксы будут такие:

"z" - для обработки целочисленных типов;
"f" - для обработки типов с плавающей точкой;
"q" - для обработки типов обыкновенных дробей.

Некоторые функции имеют модификации для работы со стандартными типами Си\Паскаль и они имеют соответствующие постфиксы после основного названия функции:

"_ui" - работают с беззнаковым целым;
"_si" - работают со знаковым целым;
"_d" - работают с типом "Double".

Опять же, в связи с многочисленностью функций, я не буду устраивать здесь русскоязычный перевод официальной документации, а расскажу только про самые необходимые на мой взгляд, которые позволят использовать специфические GMP типы данных как те, которые вы ранее неоднократно использовали в своих программах. А уж на примере этих функций вы спокойно можете по официальной документации разобраться и с другими функциями, если в них возникнет потребность.

5.1 Создание и удаление переменных

Начнём с манипуляций низкоуровневыми, сишными типами. Вкусное (интерфейсы) оставим на десерт. Переменную сначала необходимо инициализировать. При инициализации происходит выделение памяти для поля переменной "data" и запись количчества выделеной памяти в поле "allocate", если речь идёт о целочисленных типах или в "prec", если речь идёт о десятичных дробях. Для инициализации есть две функции:

префикс_init(переменная)
Здесь для переменной выделяется количество памяти заданной мантиссе по умолчанию и значение переменной становится равно "0". Умолчальное значение количества памяти - 1 лимб под мантиссу и 1 лимб под экспоненту. Для традиционных типов FreePascal соответствует целочисленному "Int64" (для 64-разрядного компилятора) или "longint" (для 32-разрядного), а вот для типов с плавающей точкой аналогов уже не имеется. Некое слабое подобие имеет тип "Extended", однако у него мантисса короче;
префикс_init2(переменная, количество_бит)
Здесь уже с самого начала предусматривается число с мантиссой большей, чем у традиционных типов. Под экспоненту так же отводится 1 дополнительный лимб. Какой длины должна быть мантисса - это нужно задать в параметре "количество_бит". Правда не совсем понятно, а скольким количествам разрядов числа будет соответствовать это самое "количество_бит". Видимо здесь разработчики пытались совместить 23-ух и 64-ёх разрядные системы, поэтому не стали в этом параметре вводить ни байты, ни лимбы. В одном из примеров для типа "mpf_t" предлагается воспользоваться формулой: Количество_разрядов = floor(количество_бит * log10(2))
Отсюда можно определить, какое количество битов требуется нужному количеству разрядов: Количество_битов = ceil(количество_разрядов / log10(2))
Чтобы зазря не расходовать драгоценные компьютерные ресурсы вычислением логарифма, в модуле "gmp.pas" есть уже соответсвующая константа - LOG_10_2.

Хочу заметить, несмотря на то, что вторая функция инициализации никоим образом не накладывает на нас ограничение на число в параметре "количество_бит" (ну, естественно, кроме того что число явно должно быть целым и неотрицательным), однако в реальности после инициализации оказывается, что это количество выравнивается по размеру лимба в большую сторону. Например, если "количество_бит" вы зададите "112", компилятор возражать этому не будет, но выделение памяти автоматически подкорректироется до цифры "128". Поэтому не заставляйте свой процессор делать лишнюю работу по коррекции числа битов, а сразу пишите это число как надо.

Специально для типа десятичных дробей существует функция, задающая "количество_бит", которое в дальнейшем будет использоваться при инициализации всех переменных по умолчанию:

mpf_set_default_prec(количество_бит)

Она должна стоять в коде до любых функций инициализации. После неё все функции mpf_init(переменная) будут задавать переменным десятичных дробей то "количество_бит", которое указано в функции. Это очень удобно.

Сколько памяти выделять для длинных чисел?
При работе с целыми числами этим вопросом в принципе можно не заморачиваться. Ну, в крайнем случае, посчитать количество разрядов которое будет у возможно самого большого числа. А если используем отрицательные числа - то у самого маленького. В этом случае мы немного съэкономим расчётное время процессора. Однако при работе с десятичными дробями этот вопрос встаёт со всей остротой. Причина тому - мантисса. К примеру, самое большое число у нас будет "2,761E+100500". Несмотря на чудовищную по размеру экспоненту, мантисса у нас махонькая. Таким образом под число будет достаточно всего одного лимба, что библиотека делает по умолчанию.
В обязательном порядке нужно:

спрогнозировать, сколько нам понадобится значащих разрядов именно для мантиссы;
пересчитать разряды в количество битов (формула дана выше);
в обязательном порядке добавить к получившемуся результату ещё столько разрядов, которое соответствует, как минимум, одному лимбу. Это на всякий случай, потому что только с "лишними" разрядами точность числа для значимых разрядов не пострадает.

После того как мы вволю попользовались "длинными" переменными их необходимо утилизировать, чтобы зря память не жрали:

префикс_clear(переменная)

5.2 Присвоение переменным значений

Следующий важнейший вид функций - присвоение значения переменной. Хотя переменным GMP-типов можно присваивать значения обычных числовых типов, но, на мой взгляд, самыми интересными является функции присвоения чисел из строки. Кроме вполне очевидного преимущества - разрядность таких чисел ограничивается лишь оперативной памятью, есть и ещё одна интересная фишка: можно вручную задать систему счисления. Хотите использовать 12-тиричную систему счисления, которой пользовались наши предки? Нет проблем.

префикс_set_str(переменная, 'Значение', Система_счисления)

Здесь "Система_счисления" может иметь значение от 2 до 62. Честно говоря с системами счисления отличными от 2, 10 и 16 я не экспериментировал, так что насколько там верен (или усложнён) счёт - проверяйте сами.

Кстати говоря, если значение "Система_счисления" поставить 0, то функция сама попытается её определить по содержимому, точнее говоря - по первым символам числа. Если первыми символами стоят "0b" или "0B", то число считается двоичным. Если "0x" или "0X", то шестнадцатиричным. Если просто "0" - то восьмиричным. Во всех остальных случаях число будет считаться десятичным.

С присвоением целых чисел я думаю непоняток не возникнет. Десятичные дроби можно записывать как в обычном формате (типа "3.141592"), так и в научном (типа "1.05457159642e-27"). Числа обыкновенных дробей можно присваивать как дробью целиком, отделяя числитель от знаменателя знаком "/", так и отдельно числитель и отдельно знаменатель:

program primer3;
Var
  Drob : mpq_t;
  num : mpz_t;
  den : mpz_t;
  
Begin
  mpq_init(Drob);
  mpz_init(num);
  mpz_init(den);
  
  // Здесь 123 - числитель, а 321 - знаменатель дроби   
  mpq_set_str(Drob, '123/321', 10);
  
  mpz_set_str(num, '123', 10);
  mpz_set_str(den, '321', 10);  
  // А можно присвоить отдельно числитель
  mpq_set_num(Drob, num);
  // И отдельно знаменатель
  mpq_set_den(Drob, den);
  
  ...  
  
  mpq_clear(Drob);
  mpz_clear(num);
  mpz_clear(den);
End.

Если присваивание завершилось благополучно, функции возвращают ноль, в противном случае - минус единицу.

Когда из дроби нужно получить целое число, можно использовать следующие функции:

mpz_set_f(Результат: mpz_t; Переменная: mpf_t)
mpz_set_q(Результат: mpz_t; Переменная: mpq_t)

При этом с дробью проводится операция аналогичная стандартной функции Trunc() в Паскале.

Для целочисленных типов и десятичных дробей есть функция, которая совмещает инициализацию переменной и присвоение значения:

префикс_init_set_str(Переменная, 'Значение', Система_счисления)

5.3 Вывод переменных на экран

Теперь пора бы вывести на экран значения переменных. Стандартными паскалевскими средствами напрямую это сделать не удасться, нужно применить специальную функцию форматированного вывода, аналогичную существующей в Си:

mp_printf('Строка_формата_вывода'[, @Переменная1, @Переменная2, ... ])

Оператор взятия адреса (@) у переменной должен присутствовать в обязательном порядке. Специально обращаю на это ваше внимание, т.к. в оригинальной документации, для языка Си, вывод значения переменной происходит без взятия адреса. "Строка_формата_вывода" формируется аналогично строке формата в Си:

%[флаги][Длина_переменной][.Количество_знаков_после_десятичной_точки][Тип_GMP]тип_Си

По сути дела эта функция представляет тип GMP в подходящий тип Си и этот тип Си выводится на экран. От стандартной сишной функции отличается только тем, что вывод GMP-переменной идёт с помощью двойного символа типа данных: первый - для GMP-типа, второй - для сишного типа. В таблице 1 представлены типы GMP и близкие типы Си:

Таблица 1. Типы GMP и близкие им типы языка Си

Наименование	Тип GMP	Тип Си
Целое	Z	d − целое десятичное, x − целое шестнадцатиричное, o − целое восьмиричное.
Десятичная дробь	F	e − с плавающей точкой в научном формате, f − с фиксированной точкой
Обычная дробь	Q	Аналогично Z. Вывод будет в виде: числитель/знаменатель

Обращаю ваше внимание, что GMP-типы всегда пишуться заглавной буквой, именно так, как указано в табл. 1.

Про вывод чисел с плавающей точкой хотелось бы сказать особо. В оригинальной документации [3, с. 72] в качестве формата "Длина_числа.Знаков_после_точки" приведена такая конструкция:

%.*Ff

Здесь звёздочка после точки предполагает, что функция сама определит длину выводимого числа и знаков после точки. У меня пару раз была ситуация, когда такой формат приводил к выводу на экран просто таки огромного количества нолей. Я не смог определить в чём тут проблема, возможно она возникает именно от того, что я использую FreePascal, а не Си. Надёжнее будет прямо указывать общее количество разрядов и количество разрядов после точки, например:

%200.100Ff

в таком формате проблем с выводом у меня ни разу не было.

Особо хочу обратить внимание на то, что сишные служебные символы, которые начинаются с "\", например перенос строки "\n", вставлять в строку формата не стоит, т.к. в Паскале они будут интерпретированы как самые обычные символы. Если требуются символы форматирования, то нужно использовать их паскалевский вид, например перенос строки:

Var
  f: mpf_t;
Begin
  ...
  mp_printf('%200.100Ff'#10, @f);
End;

Как и у всякой бочки мёда, у функции "mp_printf()" есть своя ложка дёгтя. Дело в том, что вряд ли длинные числа стоит выводить на экран, чтобы просто поглазеть на них. Скорее всего они понадобятся где-то ещё - в отчёте, в дальнейших вычислениях и т.п. Поэтому результаты нужно куда-нибудь сохранять, например в текстовый файл. Да и, откровенно говоря, хотелось бы для вывода использовать традиционные паскалевские средства, тем более что "Write\WriteLn" без больших напрягов позволяет перенаправить вывод в текстовый файл. Для этого нужно воспользоваться одной из нескольких функций библиотеки (например, "mp_sprintf()") для конвертирования получившегося числа в строку, а точнее говоря, в тип "PChar". А вот переменную этого типа уже можно спокойно вывести или на экран, или перенаправить в файл:

Var
  f: mpf_t;
  n1, n2: longword;
  pc: PChar;
Begin
  mpf_set_default_prec(256);   
  mpf_init_set_str(f, '3.141592653589793238462643383279502884197169399375105820974944', 10);
  n1 := Floor(mpf_get_prec(f) * LOG_10_2);
  n2 := n1 - 2;
  GetMem(pc, n1);
  mp_sprintf(pc, PChar('%'+IntToStr(n1)+'.'+IntToStr(n2)+'Ff'), @f);
  WriteLn(pc);
End;

Как видите, функция "mp_sprintf()" работает по тому же принципу, что и "mp_printf()", т.е. используя строку формата формирует из числа требуемую строку, которая потом выводится штатными средствами FreePascal. Поскольку в строковом представлении числа 1 байт это 1 разряд (исходим из предположения, что кодировка у нас ASCI\ANSI или UTF-8), то количество байтов для выделения памяти под строку определяем по известной нам формуле.

В приведённом выше примере для определения количества выделяемой под строку памяти использовалась функция mpf_get_prec(), Которая приведёт к тому, что в получившейся строке с числом может быть большое количество ведущих пробелов. Проблема в том, что для типа "PChar" я в модуле "strings" удалителя пробелов отчего-то не нашёл, хотя эта функция и для "PChar" была бы весьма полезна. Поэтому данные из "PChar" переношу в "AnsiString" и уж там применяю функцию "Trim()", после чего в строке остаётся только число:

Var
  f: mpf_t;
  n1: longword;
  pc: PChar;
  s: AnsiString;
Begin
  mpf_set_default_prec(256);   
  mpf_init_set_str(f, '3.141592653589793238462643383279502884197169399375105820974944', 10);
  n1 := Floor(mpf_get_prec(f) * LOG_10_2);
  GetMem(pc, n1);
  mp_sprintf(pc, PChar('%'+IntToStr(n1)+'.Ff'), @f);
  s := pc;
  s := Trim(s);   
  WriteLn(s);
End;

Рисунок 4. Вывод числа преобразованного в строку

Есть ещё одна функция преобразования числа в строку. Она более сложная, не совсем понятная, но универсальная, рассчитаная на любую поддерживаемую GMP систему счисления. Если вы неприменно захотите почитать оригинальную документацию GMP, то по поводу перевода числа в строку вам буквально сразу же на глаза попадётся функция "префикс_get_str()". И если для целых чисел и обыкновенных дробей эта функция выглядит в высшей степени великолепно, то вот для десятичных дробей не сразу и поймёшь, как её применять. Дело в том, что в получаемой строке не содержится десятичной точки. Т.е. все цифры правильные, а вот десятичной точки нет.

Честно говоря я сначала не понял, зачем вообще нужна такая функция, однако более вдумчивое её изучение показало, что позиция точки в числе может быть определена по второму параметру функции, куда возвращается величина экспоненты:

mpf_get_str(Строка: PChar; out Экспонента: mp_exp_t; СистемаСчисления: longint; КоличествоРазрядов: sizeuint; Число: mpf_t): PChar;

Положение точки для формата с фиксированной точкой вычисляется немного хитрым способом:

Нужно отсчитать от начала числа количество разрядов, которые возвращает параметр "Экспонента" и после него поставить десятичную точку.

Если вы ведёте вычисления в какой-нибудь экзотической системе счисления, вывод значения которой не поддерживается стандартом Си, то пожалуй нет никакого другого способа полюбоваться на полученое число... Если же нужно получить десятичную дробь в научном формате, то точка ставится после первого разряда, а к концу строки добавляется "Экспонента", естественно заранее отформатированнная. По сравнению с предыдущим вариантом получается сложнее, поэтому сию функцию я бы порекоммендовал применять только для получения строки целых чисел, обыкновенной дроби и десятичной дроби в формате с фиксированной точкой. Для научного формата проще использовать предыдущий вариант.

Пара интересных фишек про эту функцию:

если в первый параметр подставить "NIL", то функция сама вычислит количество памяти под строку и готовая строка с числом будет выдана в возвращаемом значении;
в отличие от предыдущего варианта перевода числа в строку, здесь строка с числом получается сразу же без всяких пробелов.

С помощью этой функции перевед десятичной дроби в строку будет выглядеть так:

Var
  f: mpf_t;
  n: longword;
  pc: PChar;
  s: AnsiString;
Begin
  mpf_set_default_prec(256);   
  mpf_init_set_str(f, '3.141592653589793238462643383279502884197169399375105820974944', 10);
  pc := mpf_get_str(NIL, n, 0, f);
  s := pc;
  s := Insert('.', s, n+1);   
  WriteLn(s);
End;

Почём, купец, экспонента?
Вышеприведённая функция прекрасно поясняет, почему разработчики не уделили внимания выделению памяти под экспоненту. Дело в том, число в сыром виде хранится именно так, как её выдаёт функция mpf_get_str(), т.е. в виде последовательности цифр. Если нам нужно научное представление числа, т.е. число с экспонентой, то величина экспоненты всегда вычисляема и зависит исключительно от того, в какое место числа мы захотим поставить десятичную точку. Не исключено, что когда-то в стародавние времена, в самых первых версиях GMP, поле "exp" соответствовало своему назначению и содержало реальное значение величины экспоненты. Но на сегодняшний день оно, похоже, осталось исключительно из совместимости со старыми версиями программ.

5.4 Арифметические операции

Теперь можно приступать к вычислениям. Операции "+", "-", "*":

префикс_add(Результат, Переменная1, Переменная2)
префикс_sub(Результат, Переменная1, Переменная2)
префикс_mul(Результат, Переменная1, Переменная2)

Операцию деления без проблем можно применять только к дробям:

mpf_div(Результат, Переменная1, Переменная2)
mpq_div(Результат, Переменная1, Переменная2)

Целочисленное же деление довольно сложное и сопряжено с многочисленными трудностями, пакостями и прочими приводящими в неописуемый ужас последствиями. Функций для целочисленного деления очень много. Условно их можно разделить на следующие группы:

Каким образом округляется результат. Согласитесь, без округления в целочисленном делении обойтись можно очень редко. Каким образом округляется результат, можно определить по основному названию функции:
- mpz_cdiv_постфикс(Результат, Делимое, Делитель) - результат округляется вверх. Соответствует паскалевской функции Ceil();
- mpz_fdiv_постфикс(Результат, Делимое, Делитель) - результат округляется вниз. Соответствует паскалевской функции Floor();
- mpz_tdiv_постфикс(Результат, Делимое, Делитель) - у результата просто обрезается дробная часть. Соответствует паскалевской функции Trunc()
Может показаться, что у второго и третьего пункта результат будет одинаковый, однако на самом деле это не так. Одинаковым он будет, если и делимое и делитель лежат на положительной оси. если по разную сторону от нуля или на отрицательной оси, то результат будет разный.
Что мы хотим получить в результате. Определяется постфиксом после основного названия:
- mpz_название_q(Результат, Делимое, Делитель) - в результате мы увидим частное;
- mpz_название_r(Результат, Делимое, Делитель) - в результате мы увидим остаток от деления;
- mpz_название_qr(Результат1, Результат2, Делимое, Делитель) - в Результат1 увидим частное, в Результат2 увидим остаток от деления.
Ряд специфических функций, которые могут быть полезны только при определённых условиях. Например, следующая функция определена разработчиком как "быстро работающая" в отличие от предыдущих:
- mpz_divexact(Результат, Делимое, Делитель)
Правильный результ с её помощью можно получить только при условии что "делитель" является чётным числом, а если это не так, то заранее должно быть известно, что "Результат" будет именно целочисленным. Во всех остальных случаях в "Результате" вы получите чёрте что и сбоку бантик.

Порою черезвычайно полезными бывают функции возведения в степень и извлечения квадратного корня. Представлены они только для целого типа и типа десятичной дроби:

префикс_pow_ui(Результат, Переменная, Показатель_степени)
префикс_sqrt(Результат, Переменная)

"Показатель_степени" в первой функции должен быть стандартного паскалевского целого типа без знака.

А вот здесь настало время вернуться к пугалкам, кряхтелкам и страшилкам по поводу нехватки памяти в переменной, чтобы вместить туда получившийся после вычислений ответ. Естественно, речь пойдёт только о десятичных дробях. Самыми вероятными кандидатами из арифметических операций, которые дадут эффект "невлезания" ответа в переменную - это умножение и возведение в степень. Подсчитать требуемое количество разрядов числа под ответ можно довольно простым, хотя и пессимистическим, способом:

Для операции умножения. Нужно сложить количество разрядов всех чисел, которые участвуют в умножении и таким образом получим количество разрядов, куда гарантированно влезет ответ;
Для операции возведения в степень. Умножим количество разрядов числа возводимого в степень на показатель степени.

Далее, количество разрядов переводим в биты:
Количество_бит = Ceil(Количество_разрядов / LOG10(2))
Заранее согласен, что алгоритм не блещет точностью, однако он гарантированно не даст обрезать цифры в ответе.

5.5 Сравнительные операции

Функции сравнения чисел:

префикс_cmp(Переменная1, Переменная2): integer;

Возвращает:

1, если Переменная1 > Переменная2;
0, если Переменная1 = Переменная2;
-1, если Переменная1 < Переменная2.

5.6 Диагностика и выуживание стандартных типов

Функция проверки знака числа:

префикс_sgn(Переменная): integer;

Возвращает:

1, если Переменная > 0;
0, если Переменная = 0;
-1, если Переменная < 0.

Следующую группу функций можно назвать диагностической. Она может пригодиться в том случае, если необходимо будет конвертировать типы данных GMP в стандартные типы данных. Она применяется только для целых чисел и десятичных дробей и определяет, сможет ли число из проверяемой переменной влезть в один из стандартных типов:

префикс_fits_ushort_p (Переменная): integer; - для беззнакового байта;
префикс_fits_sshort_p (Переменная): integer; - для байта со знаком;
префикс_fits_uint_p (Переменная): integer; - для беззнакового целого;
префикс_fits_sint_p (Переменная): integer; - для целого со знаком;
префикс_fits_ulong_p (Переменная): integer; - для беззнакового длинного целого;
префикс_fits_slong_p (Переменная): integer; - для длинного целого со знаком.

Возвращает 0, если число в "Переменная" в указаный тип не помещается и 1 - если помещается.

mpf_integer_p(Переменная): integer; - возвращает 1 если число в "Переменная" является целым и 0 в противном случае.

Само преобразование в один из стандарных типов для десятичных дробей и целых чисел можно сделать функциями:

префикс_get_si(Переменная): longint; - возвращает знаковое целое;
префикс_get_ui(Переменная): longword; - возвращает беззнаковое целое;
префикс_get_d (Переменная): double; - возвращает тип "double";

Из обыкновенной дроби можно получить только тип "double":

mpq_get_d (Переменная): double;

5.7 Немного практики

Попробуем изобразить что-то серьёзное, например генератор псевдослучайных чисел с равномерным распределением в интервале от 0 до 1. Оригинал кода я стыбрил в библиотеке численных методов НИВЦ МГУ [4] и единственное, что мне там не понравилось в ихнем изложении кода для Паскаля - использование типа "Extended". Однако если подсчитать разрядность мантиссы константы D2PN31, то окажется, что типом "Double" здесь никак не обойтись. Следовательно эта процедура явный кандидат на использование совместно с GMP. Впрочем, данный пример имеет скорее учебный, чем реальный смысл, т.к. в библиотеке GMP есть собственные функции генератора псевдослучайных чисел.

{$mode objfpc}
program primer4;
Uses gmp;

{ Остаток от деления для нецелых чисел, согласно фортрановской документации
  (т.к. Паскаль подобных операций не предусматривает):
  result := Arg1 - ( int(Arg1/Arg2) * Arg2) }
function Emod(Arg1, Arg2 : mpf_t): mpf_t;
Var
  f: mpf_t;
begin
  mpf_init(f);
  mpf_init(Result);
  mpf_div(f, arg1, arg2);
  mpf_trunc(f, f);
  mpf_mul(f, f, arg2);
  mpf_sub(Result, arg1, f);
  mpf_clear(f);
end;

{Вычисление псевдослучайных чисел с равномерным распределением
 в диапазоне от 0 до 1.
 Входные параметры:
	ISEED - целая переменная, значение которой перед обращением 
		к подпрограмме может быть любым целым числом в пределах 
		[1 ... 2147483646]; по окончании работы ее значение полагается 
		равным (2^31) * R (N), и это значение может быть использовано 
		при последующем вхождении в подпрограмму;
	N - 	заданное количество генерируемых псевдослучайных чисел (тип: целый);
	R - 	вещественный массив длины N, содержащий вычисленные псевдослучайные числа.} 
procedure GSU1R(var ISEED :longword; N :Integer; var R :Array of mpf_t);
var
  I		: Integer;
  Z		: mpf_t;
  D2P31M	: mpf_t;
  D2PN31	: mpf_t;
  
const
  D2P32M :Integer = 16807;

begin
  mpf_init_set_str(D2P31M, '2147483647.0', 10);
  mpf_init_set_str(D2PN31, '4.656612873077393e-10', 10);
  mpf_init_set_ui(Z, ISEED);
  for I:=0 to N-1 do
  begin
    mpf_mul_ui(Z, Z, D2P32M);
    Z := Emod(Z,D2P31M);
    mpf_mul(R[I], Z, D2PN31);
  end;
  ISEED := mpf_get_ui( Z );
end;

var
  ISEED,N, i :longword;
  R :Array [0..2] of mpf_t;
begin
  ISEED := 123457;
  N := 3;
  For i:=0 To N-1 Do
    mpf_init(R[i]);
  GSU1R(ISEED,N,R);
  for i:=0 to 2 do
    mp_printf('%20.10Ff'#10, @r[i]);
end.

Рисунок 5. Результат работы генератора псевдослучайных чисел с использованием GMP-типов

Для целых чисел и десятичных дробей в GMP есть собственная функция генератора равномерно распределённых псевдослучайных чисел:

префикс_urandomb(Результат, Инициатор, Количество_битов_в_числе): integer;

Для целых чисел генерирует псевдослучайное число от 0 до 2n-1, где n - это "Количество_битов_в_числе". Для десятичных дробей - число от 0 до 1, с мантиссой размером в "Количество_битов_в_числе".

"Инициатор" - это специальный тип-запись, который хранит в себе число-инициализатор и номер алгоритма генерации псевдослучайного числа:

  randstate_t = record
    seed: mpz_t;
    alg : randalg_t;
    algdata: record
      case longint of
        0 : (lc : pointer);
    end;
  end;

Значение переменной этого типа задаётся специальными процедурами, в зависимости от типа алгоритма генерации. Самая простая функция:

procedure mp_randinit_mt(out state: randstate_t);

задаёт алгоритм Мерсена-Твистера, который считается самым быстрым.

После использования - обязательная зачистка:

procedure mp_randclear(var state: randstate_t);

А теперь представим тот же самый пример, но с использованием высокоуровневых типов-интерфейсов:

{$mode objfpc}{$H+}
program primer4;
Uses gmp;

{ Остаток от деления для нецелых чисел, согласно фортрановской документации
  (т.к. Паскаль подобных операций не предусматривает):
  result := Arg1 - ( int(Arg1/Arg2) * Arg2) }
function Emod(Arg1, Arg2 : MPFloat): MPFloat;
Var
  f: MPFloat;
begin
  f := Arg1/Arg2;
  Result := Arg1 - ( f_trunc(f) * Arg2);
end;

{Вычисление псевдослучайных чисел с равномерным распределением
 в диапазоне от 0 до 1.
 Входные параметры:
    ISEED - целая переменная, значение которой перед обращением 
	к подпрограмме может быть любым целым числом в пределах 
	[1..2147483646]; по окончании работы ее значение полагается 
	равным (2^31) * R (N), и это значение может быть использовано 
	при последующем вхождении в подпрограмму;
    N - 	заданное количество генерируемых псевдослучайных чисел (тип: целый);
    R - 	вещественный массив длины N, содержащий вычисленные псевдослучайные числа.} 
procedure GSU1R(var ISEED :longword; N :Integer; var R :Array of MPFloat);
var
  I		: Integer;
  Z		: MPFloat;
  D2P31M	: MPFloat;
  D2PN31	: MPFloat;
  
const
  D2P32M :Integer = 16807;

begin
  D2P31M := '2147483647.0';
  D2PN31 := '4.656612873077393e-10';
  Z := ISEED;
  for I:=1 to N do
  begin
    Z := Z * D2P32M;
    Z := Emod(Z, D2P31M);
    R[I-1] := Z * D2PN31;
  end;
  ISEED :=  Z;
end;

var
  ISEED,N, i :longword;
  R :Array [0..2] of MPFloat;
begin
  ISEED := 123457;
  N := 3;
  
  GSU1R(ISEED,N,R);
  for i:=0 to 2 do
    WriteLn(string(r[i]));
end.

Как видим, код стал выглядеть намного проще. Вместо специальных функций, над переменными-интерфейсами можно применять обычные арифметические операторы. Вдобавок и вывод результата можно делать стандартными паскалевскими методами, правда не забыв привести к типу "String". Однако здесь есть один подводный камнь, не зная которого можно долго пялиться в сообщения об ошибке на этапе компиляции и ничего не понять.

В функции Emod() и в цикле процедуры GSU1R() если бы мы применяли стандартные типы данных, то количество строк можно было бы сократить на одну штуку:

Result := Arg1 - ( f_trunc(Arg1/Arg2) * Arg2);

...

for I:=1 to N do
begin
    Z := Emod(Z * D2P32M, D2P31M);
    R[I-1] := Z * D2PN31;
end;

Однако в документации [3, с. 88, 89] написано, что когда мы работаем с классами или интерфейсами, то передавать в функции вычисляемые параметры с их участием ни в коем случае нельзя. Именно поэтому пришлось вводить дополнительные строки с предварительным вычислением.

Вот что у нас в результате получилось:

Рисунок 6. Результат работы генератора псевдослучайных чисел с использованием высокоуровневых GMP-типов

Как видно, из-за увеличения количества разрядов, второй и третий результат слегка отличаются от работы предыдущей версии программы. Но совпадение очевидно, просто в прошлый раз получилось меньшее количество разрядов, из-за чего результаты подверглись округлению.

6. Скорость работы GMP

А то как же? Ведь вычислительная техника с самого начала предполагала увеличение скорости вычислений. Причём чем больше, тем лучше. Это как раз тот случай, когда "размер имеет значение". А вот когда вычислительная техника перебралась в автоматику, от неё стали требовать работу не "быстрее", а "вовремя". Но сейчас нас интересует именно скорость.

Для определения скорости обычно берут какую-нибудь черезвычайно большую систему линейных уравнений, а потом выводят некий весьмя подозрительный коэффициент - Гига\ПетаФЛОпСы. Это как в известном мультфильме - измерение питона в попугаях. Однако на самом деле интерес представляет только скорость решения этой системы. В отличие от тестов суперкомпьютеров, я возьму любимую многими задачу - вычисление числа "PI". И поскольку вычисление будет происходить на компьютере, а не вручную или на калькуляторе, то и алгоритм будет сложный, итерационыый, например формула Фабриса Беллара [5]:

Рисунок 7. Формула вычисления числа PI Фабриса Беллара

Объектами сравнения будут:

Программа от FreePascal:
- Для низкоуровневых типов GMP;
- Для высокоуровневых типов GMP;
- Для стандартных типов данных;
Программа от GCC:
- Для низкоуровневых типов GMP;
- Для высокоуровневых типов GMP;
Программа от GFortran:
- для стандартных типов данных.

GFortran я сюда присовкупил исключительно как эталон скорости вычислений, потому что в чисто вычислительных задачах, хоть GNU Си почти наступает Фортрану на пятки, но вот сравниться с ним по скорости пока получается не очень часто. Однако ещё более интересной особенностью GFortran, как раз для данного случая, является его способность без малейших усилий игнорировать переполнение, которое возникнет при вычислении переменной "m1" (см. исходный код ниже, целиком исходники в архиве [8]) примерно на сотой с чем-то итерации. Нет, не надо думать, что Фортран его не заметил, просто в нашем случае переполнение никоим образом на результат не повлияет, зато можно спокойно просимулировать большое количество итераций. А вот аналогичный код на FreePascal заставит программу падать в обморок. Поэтому данный участок кода пришлось обрамить конструкцией "Try ... Except", что естественно скорости не добавляет, но способствует продолжению вычислений. Правда смысл большого количества итераций именно для ответа теряется (так же как в коде Фортрана), зато удаётся эти самые итерации симулировать, что для теста как раз и требуется.

Результат вычисления мы будем сравнивать с числом "PI" из Википедии [6], где это число приводится с первой тысячью знаков после запятой.

Итак, программа с применением стандартных типов данных FreePascal:

For k:=0 To 20000000 Do
  Begin
    Try
      m1 := Power(-1.0, k)/Power(2.0, (10.0*k));
    except
    end;
    m2 := -(Power(2.0, 5.0)/(4.0*k + 1.0));
    m3 := 1.0/(4.0*k + 3.0);
    m4 := Power(2.0, 8.0)/(10.0*k + 1.0);
    m5 := Power(2.0, 6.0)/(10.0*k + 3.0);
    m6 := (2.0 * 2.0)/(10.0*k + 5.0);
    m7 := (2.0 * 2.0)/(10.0*k + 7.0);
    m8 := 1.0/(10.0*k + 9);
    pi_bellard := pi_bellard + m1 * (m2 - m3 + m4 - m5 - m6 - m7 + m8);
  end;
pi_bellard := pi_bellard * 1.0/Power(2.0, 6.0);

Количество итераций сравнительно небольшо - 20 000 000, потому что тестирование будет проходить на малохольном ноутбуке с процессором Intel Pentium 3825U 1.9 ГГц. Расчёт формулы я разделил на несколько логически обособленных подформул, потому что в длинных формулах постоянно путаюсь. Но ещё более важная причина разделения - иллюстрация чуть ниже необходимости применения в подобных расчётах одинаковых типов данных. Результат работы такой программы представлен на рис. 8:

Рисунок 8. Число PI. FreePascal со стандартным типом "Extended"

Здесь и на следующих рисунках:

первое число - результат вычисления числа "PI";
второе - время вычисления;
третье - число "PI" из Вики, для сравнения.

Результат, по точности, отличный. Последнюю ненулевую цифру во внимание, естественно, не принимаем, т.к. она, по определению, неточная. Для сравнения - фортраньи вычисления:

Рисунок 9. Число PI. GFortran со стандартным типом "REAL(16)"

Чисто теоретически, на тип длинного числа вполне хватит поменять переменную "m1", т.к. только в ней возникает переполнение, вне зависимости от применённых компиляторов.

Var
  pi_bellard: MPFloat;
  m1, m2, m3, m4, m5, m6, m7, m8: MPFloat;
  tmp1, tmp2: MPFloat;
  startt, endt: TDateTime;
  k: longword;

Begin
  f_set_default_prec(128);
  
  pi_bellard := 0.0;

  tmp1:='-1.0';
  tmp2:='2.0';
  
  For k:=0 To 20000000 Do
  Begin
    m1 := f_pow_ui(tmp1, k)/f_pow_ui(tmp2, (10*k));

    m2 := -(Power(2, 5)/(4*k + 1));
    
    ...
    
  end;
  pi_bellard := pi_bellard * 1.0/Power(2.0, 6.0);

После этого программа начнёт без проблем считать, но вот точность результата заметно хромает:

Рисунок 10. Результат расчёта числа PI с частичным применением GMP

А ведь мы вводили GMP именно в надежде на точность. За объяснениями далеко ходить не надо. Чтобы получить максимально точной результат, все числа, участвующие в вычислениях, должны быть одного типа. А у нас тут сплошь и рядом применяются константы, которые компилятор FreePascal приводит либо к типу "Extended", либо к типу "Double", в зависимости от разрядности компилятора. Вот они то и дают постепенно накапливающуюся ошибку. Поскольку объявить типизированные константы "MPFloat" у нас не получится, а приводить их к этому типу прямо в коде - вид его сразу сделается ужасен, то введём дополнительные переменные, которые будут использоваться вместо констант:

Var
  pi_bellard: MPFloat;
  m1, m2, m3, m4, m5, m6, m7, m8: MPFloat;
  tmp_1, tmp1,tmp2,tmp3,tmp5,tmp7,tmp9: MPFloat;
  startt, endt: TDateTime;
  k: longword;

Begin
  f_set_default_prec(128);
  
  pi_bellard := '0.0';

  tmp_1:='-1.0';
  tmp1:='1.0';
  tmp2:='2.0';
  tmp3:='3.0';
  tmp5:='5.0';
  tmp7:='7.0';
  tmp9:='9.0';
  
  For k:=0 To 20000000 Do
  Begin
    m1 := f_pow_ui(tmp_1, k)/f_pow_ui(tmp2, (10*k));
    m2 := -(f_pow_ui(tmp2, 5)/(4*k + tmp1));
    m3 := tmp1/(4*k + tmp3);
    m4 := f_pow_ui(tmp2, 8)/(10*k + tmp1);
    m5 := f_pow_ui(tmp2, 6)/(10*k + tmp3);
    m6 := f_pow_ui(tmp2, 2)/(10*k + tmp5);
    m7 := f_pow_ui(tmp2, 2)/(10*k + tmp7);
    m8 := tmp1/(10*k + tmp9);
    
    pi_bellard := pi_bellard + m1 * (m2 - m3 + m4 - m5 - m6 - m7 + m8);
  end;
  pi_bellard := pi_bellard * tmp1/f_pow_ui(tmp2, 6);

И вот что получается в результате:

Рисунок 11. Результат расчёта числа PI с полным применением GMP

Красотища! Правда возросло время расчёта, но это и неудивительно, т.к. сложных типов данных сильно прибавилось. Зато результат один-в-один, как в Вики. Понятно, что код программы можно ещё оптимизировать, дабы получить лучшее время расчёта, но для сравнительных тестов подобный код тоже годиться. Результаты приведены в таблице 2:

Таблица 2. Сравнительные результаты тестов скорости выполнения программ без GMP и с GMP

	GFortran	FreePascal			GCC
	Стандартные типы данных	Стандартные типы данных	Низкоуровневые типы GMP	Высокоуровневые типы GMP	Низкоуровневые типы GMP	Высокоуровневые типы GMP
Время счёта, сек	86	93	134	263	134	253

Думаю что результаты тестов поклонников FreePascal должны порадовать. Несмотря на то, что компиляторы языка Си по идее должны делать более быстрые программы, однако в данном случае FreePascal показал себя нисколько не хуже. Запускайте этот тест на своём компьютере, а потом сравнивайте с результатами аналогичного вычисления, которые собирают на своём сайте разработчики [11].

7. Сборка библиотеки GMP вручную

Очень полезное заняте для тех, кто хочет добиться максимальной производительности. Дело в том, что для репозиториев ОС программы и библиотеки собираются с тем расчётом, чтобы они работали на любом компьютере, куда сия система в принципе ставится. А вот скрипт "configure", который идёт в комплекте с исходным кодом, исследует именно ваш компьютер и составляет "Makefile" с учётом особенности вашей конкретной системы. К примеру, вместо унивесального компилятора "gcc", у вас будет стоять более ловкий и пронырливый интеловский компилятор, который по идее должен сделать бинарник максимально проворным, учитывая все особенности ассемблера для интеловского процессора...

Скачать исходники GMP можно с официального FTP-сервера GNU [7]. Для сборки нам потребуется компилятор "gcc" (а если нужно программировать и в Си++, то ещё и "g++"). Поскольку половина функций GMP написана на ассемблере, то потребуется еще и стандарный GNU ассемблер "as". Вручную я его никогда не ставил, обычно при установке "gcc" он ставится сам собою. Если вы собираетесь работать с лучшей по скорости библиотекой MPIR, то вместо "as" там используется ассемблер "yasm" и вот его уже надо будет ставить ручками. Поскольку разные ОС (имеется в виду ОС Linux или BSD) формируют джентельменский набор программ по разному, исходя из каких-то своих критериев, то может понадобиться что-то ещё. Это выясняется после запуска скрипта "configure".

Один важный момент для пользователей Linux\BSD - в 99% случаев GMP у вас уже будет стоять по умолчанию из репозитория, поэтому лучше её предварительно удалить. Обычно жёстких зависимостей с каким либо пакетом я у неё не наблюдал, поэтому опасаться, что вместе с GMP удалится ещё что-нибудь, не стоит. Если вы не захотите удалять штатную библиотеку, то проблема может быть такая - по умолчанию "make install" установит вновь собранную библиотеку в "/usr/local/lib[64]", что очень удобно для отслеживания программ устанавливаемых вручную. А если в "/usr/lib[64]" будет стоять штатная библиотека, то новую использовать вам вряд ли удасться без ручного указания её в опциях компилятора.

Обычно сборка проходит без малейших затруднений. Если "configure" вам посоветовал что-то поставить - ставьте. Алгоритм сборки обычный:

./configure
make
make check
make install

Последний пункт пользователям Linux\BSD нужно делать с правами "root". А вот для для пользователей Windows этот пункт необязателен. Лучшим вариантом в Windows будет положить получившуюся библиотеку в каталог с программой.

Пункт "make check" не обязателен, но желателен. По крайней мере разработчики рекомендуют его использовать. В этом пункте выполняется несколько десятков тестов различных встроенных в GMP функций. Сами тесты находятся в каталоге исходного кода, в подкаталоге "tests".

Ещё пара рекоммендаций для сборки в Windows. Лучше всего это делать совместно с "mingw", т.к. эта среда ближе всего к Windows, как минимум в плане кодировки русского языка. И есть ещё один нюанс в плане получающегося результата. Несмотря на то, что сборка вместе с "cygwin" проходит успешно, получить работающее приложение мне не удалось. Вполне возможно не хватает чего-то специфического, "cygwin'овского", но ошибок никаких не выдаётся, просто программа висит и не работает. С "mingw" таких непоняток не наблюдается.

Второй нюанс (вне зависимости от использования "cygwin" или "mingw") - результатом сборки будет только статическая библиотека. Чтобы получить динамическую библиотеку, запустите "configure" с ключом:

./configure --enable-shared

И если статическая библиотека вам не нужна, то с такими ключами:

./configure --enable-shared --disable-static

Дальше - как обычно.

После сборки библиотеки, её нужно переименовать в "gmp.dll" и добавить из состава "mingw" библиотеку "libgcc_s_dw2-1.dll", если вы свою программу собираетесь отдавать кому-то на сторону. Если же будете пользоваться только у себя, то вполне достаточно путь к этой библиотеке добавить в переменную "PATH".

8. Как сделать gmp.pas посовременнее

Посовременнее - естественно с точки зрения современного Паскаля. С одной стороны, использование низкоуровневых, сишных типов данных весьма благоприятно сказывается на скорость выполнения программ. (см. пункт "Скорость работы GMP"). А с другой стороны FreePascal, в отличие от Си, спокойно позволяет перегружать функции и операторы, таким образом позволяя приблизить вид программного кода со сложными, нестандартными данными к виду со стандартными. Как раз в этом направлении для пользователей FreePascal есть очень неожиданная, но приятная новость: оказывается, если сипользовать FCL'ный "gmp.pas", то арифметические операторы спокойно можно применять при манипуляции с низкоуровневыми типами. В Си такого сделать не получится. Почему такая благость для FreePascal - мне непонятно. Однако хочу сразу предупредить, что пользоваться этой возможностью нужно с изрядной осторожностью. К примеру, если в программе есть цикл с достаточно большим количеством итераций (естественно само поняте "достаточно большое количество" напрямую зависит от количества обрабатываемых переменных внутри цикла и от количества операций с ними), то в мониторинге производительности можно увидеть, что с каждой итерацией возрастает потребление оперативной памяти. В случае же использования для того же алгоритма в качестве арифметических операций функций библиотеки, такого явления не наблюдается.

На github я выложил обновлённый модуль "gmp.pas" [9]. Модуль сделан на основе последней на момент написания статьи версии библиотеки GMP - 6.1.2. В нём сделаны следующие изменения по сравнению с уже имеющимся в FreePascal:

Добавлены функции инициализации (и очистки) неопределённого количества переменных за раз (префикс_inits() и префикс_clears()) которые появились в версии 5 библиотеки GMP. В FCL'евской "gmp.pas" они отсутствуют;
Добавлена функция префикс_sgn() позволяющая определить знак числа. В самой библиотеке её нет, но макрос определён в "gmp.h". Такой уж насущей необходимостью она не является, т.к. знак числа можно определить по полю "size" переменной. Но пусть будет на всякий случай;
Добавлены типы данных, которые были в "gmp.h", однако по какой-то причине отсутствовали в старом "gmp.pas";
Все типы параметров функций приведены к единому стандартному виду. Дело в том, что в старом модуле "gmp.pas" встречались параметры дополненные модификатором "var" в том случае, если функция их изменяет. Новые функции, типа префикс_inits() с таким модефикатором работать отказываются. Вдобавок встречаются функции (типа gmp_printf()) в которых параметры непременно нужно указывать в виде адреса. В новом модуле этот разнобой устранён. Все параметры требующие длинные числа передаются функциям как адрес с помощью "@". Заранее согласен, что конкретно для языка Паскаль такая передача параметров выглядит совершенно нетипичной. Но, к большому сожалению, не все сишные функциии библиотеки GMP работают с модификатором "var";
Все имена функций приведены к виду, описанному в оригинальной документации. Таким образом, не будет каких-либо излишних проблем, чтобы существующий сишный код быстро переделать в паскалевский;
Параметры длинных чисел, которые не требуют изменения, дополнены модификаторм "const", как это сделано в оригинальном коде библиотеки;
В модуль не включены некоторые функции из "gmp.h", которые используют специфичные для Си типы данных, например "FILE" или "va_list". Хотя включить в модуль аналог сишного "FILE" не составляет труда, однако проблемы будут у самой библиотеки GMP. Дело в том, что у разных компиляторов Си структура типа "FILE" разная. Даже, как ни странно, у "mingw" и "cywin" у которых, казалось бы, компилятор один и тот же - "gcc";
Все функции, которые у разработчиков в документации помечены как "устаревшие", снабжены меткой "deprecated" на которую компилятор "fpc" будет выдавать предупреждение с рекомендацией чем можно заменить;
В модуль не включено всё, что касается ООП. Дело в том, что ООП в в FCL'евском модуле - это чистая отсебятина, которая к оригиналу не имеет ни какого отношения. И вдобавок, работа с этими объектами строится не на метоодах класса, а на обычных функциях. Как упроститель кода - хорошее решение, вот только к ООП это имеет весьма отдалённое отношение.
Но это не главное. Исследование интернета показало, что даже те разработчики, которые в своих проекта с GMP используют компиляторы C++, предпочитают применять низкоуровневые, сишные типы данных. Причина тому очень наглядно представлена в табл. 2

Все функции разделены на несколько включаемых файлов:

mpf.inc - функции относящиеся к десятичным дробям;
mpn.inc - низкоуровневые функции. Эти функции непосредственно в программе с длинными числами не используются. Однако если есть необходимость сократить время исполнения чего-либо, то можно их применить;
mpq.inc - функции обычных дробей;
mpz.inc - функции для целых чисел;
print.inc - общие функции относящиеся к вводу\ввыводу данных;
random.inc - функции обслуживающие генераторы псевдослучайных чисел.

Такое разделение сделано на тот случай, если вы захотите сэкономить на размере программы, применяя только один тип данных. Например, если вам нужны только целочисленные вычисления, то в файле "gmp.pas" нужно закомментировать строки "{$include mpf.inc}", "{$include mpq.inc}", "{$include mpz.inc}". Вот кстати, в самой GMP, в исходном коде, предлагается ещё и модуль "mini-gmp", который так же предлагает урезаный функционал только для целочисленных типов данных.

Все примеры из статьи будут прекрасно работать с новым модулем, если параметры длинных чисел передавать в функции через "@".

В дополнение к "gmp.pas", предлагается модуль "gmp2.pas". В этом модуле я постарался сделать использование GMP более удобным, чем это предлагается в оригинале "gmp.h". Вот основные дополнения:

Определены операторы присваивания всех основных стандартных типов переменным GMP;
Определены операторы сравнения переменных GMP;
Кое-какие процедуры сделаны функциями;
Добавлены кое-какие информационные функции, например расчёта количества разряда в числе или максимальное количество разрядов, которое можно получить в представленном числе.

В архиве с исходниками приложенном к статье [8] модуль "gmp2.pas" предназначен для старого, FCL'евского модуля "gmp.pas". На [9] этот модуль уже только для нового "gmp.pas".

9. Заключение

Так где же можно использовать эту библиотеку? На самом деле, если её просто так воткнуть в вычисление вместо обычных типов, то скорость расчётов, как показали тесты, упадёт. Наибольшая её полезность будет в тех расчётах, где для требуемой точности результата длины мантиссы стандартных типов не хватит. Например, такое обязательно случится там, где одновременно исользуются очень маленькие и очень большие числа, а применение приставок (кило-, мега-, нано-) эффетка не дадут. Например, воздействие молнии (у которой напряжение несколько миллионов вольт и оно известно с точностью до последнего знака) на одну молекулу воды (размером в пару нанолитров). Обычные типы данных совместить такую разность в числах нам не дадут. Хотя программа ругаться не будет, но выдадаст результат, которой даже и близко с правильным не валялся.

При использовании десятичных дробей нужно очень внимательно подойти к выбору размера хранилища для чисел. В отличие от типа целых чисел или обычных дробей, для типа десятичных дробей не предусмотрено автоматической коррекции размера хранилища.

Чтобы быть уверенным в точности вычислений, входные данных лучше всего брать в текстовом виде или в виде целых чисел стандартных типов. В самом крайнем случае можно брать из типа "Double", но здесь уже гарантии в точности исходных данных не будет. На использование типов "Extended" или "Single" - полный запрет.

Для сохранения точности результата вычисления, размер хранилища для данных нужно обязательно брать с запасом, чтобы все значимые разряды мантиссы гарантированно туда влезали и, опять же, с запасом. Это как раз тот случай, когда "запас карман не тянет".

Наверняка вы заметили, что в библиотеке GMP есть функции, которые начинаются с префикса "mpn" и о которых я ни словом не упомянул. Дело в том, что эти функции манипулируют "лимбами", точнее хранилищами данных для "mpz_t", "mpq_t" и "mpf_t". В библиотечной иерархии они считаются "низкоуровневыми" и не предназначеными для непосредственного употребления в программах. Однако их можно применять, если вы хотите улучшить какую-либо функцию или для написания функции, которой в библиотеке раньше не было.

Библиотека GMP не единственная доступная в Паскале для работы с длинными числами. Есть модуль "MPArith" [13] Вольфганга Эрхардта, который изначально был написан в Borland Pascal и, говорят, до сих пор может там компилироваться. На сегодняшний день этот модуль можно применять в BP, Delphi и FreePascal. Работает на тех же принципах, что и GMP.

Несмотря на обилие функций в библиотеке GMP (в статье показан самый миниммум, в реальности их куда больше), может возникнуть мысль о её неполноте. На самом деле это не так. GMP задумывалась лишь как минимальный чемоданчик, обеспечивающий арифметику и логику работы с длинными числами, не более того. Если вам необходимо что-то типа паскалевского модуля "Math", то добро пожаловать в другую библиотеку - MPFR, в которой определён уже другой минимум - элементарных математических функций, типа синус-косинус-логарифм. О ней будет рассказано в следующей статье цикла.

10. Ссылки

FPC	3.2.2	release
Lazarus	3.2	release
MSE	5.10.0	release
fpGUI	1.4.1	release

links