Публикации
 FreePascal
FreePascal
FreePascal для учёных и инженеров |
06.05.2019 Вадим Исаев |
- Аннотация
- Введение
- Исследуем FCL
- ucomplex.pp. Работа с комплексными числами
- Шифрование и прочие шпионские штучки
- gmp.pas. Библиотека для работы с очень большими числами
- fftw_s.pas. Быстрое преобразование Фурье (БПФ)
- NumLib - cерьёзная математика
- Сторонние библиотеки
- Старинные, но работающие библиотеки
- Turbo Pascal Numerical Methods Toolbox
- Библиотека численного анализа НИВЦ МГУ
- Numerical Recipes
- Numerical methods
- Compact numerical methods for computers. Linear algebra and function minimisation
- Современные библиотеки
- tpmath\dmath\lmath - три имени одной библиотеки
- Alglib - с миру по нитке
- Wolfgang Ehrhardt
- Старинные, но работающие библиотеки
- Какую библиотеку выбрать?
- P.S. Внешние библиотеки. Зона особого внимания!
- Заключение
- Ссылки
1. Аннотация
Краткий обзор математических возможностей FreePascal, как с помощью стандартных средств FCL, так и с помощью внешних библиотек.
2. Введение
На сегодняшний день моделирование тех или иных процессов уверенно переселилось из области натурных экспериментов в область компьютерных вычислений. И действительно, вместо того, чтобы испортить кучу дорогостоящей техники и материалов (если у нас ничего не получится) лучше заранее знать об этом. И в этом нам помогает многочисленный и разветвлённый математический аппарат с помощью которого пусть и не просчитаешь всё на свете, но можно хотя бы спрогнозировать, что получится из тех или иных умственных выкрутасов.
Не знаю как вы, но я к вопросам программирования отношусь чисто потребительски, т.е. предпочитаю пользоваться готовыми решениями, а не выдумывать что-то самому. Ну правда, зачем расписывать функцию вычисления синуса, мучительно вспоминая, каким образом она высчитывается, если есть уже готовая в модуле "Math"... В принципе, любой язык программирования предоставляет достаточные средства для элементарных математических вычислений. Проблемы начинаются, когда мы хотим решить задачу среднего и высокого уровня. Как пример, для среднего уровня можно привести решение систем линейных/нелинейных уравнений (СЛАУ\СНАУ) или обыкновенных дифференциальных уравнений (ОДУ), на которых строится уже высокий уровень - решение конкретной физической или математической проблемы. Из примеров задач высокого уровня - моделирование старта ракеты, которое строится на решении системы ОДУ или решение задач оптимизации, которое строится на СЛАУ\СНАУ.
Может показаться, что FreePascal безнадёжно уступает таким мастодонтам численных математических методов, как MATLAB или его бесплатным аналогам SCILAB и GNU OCTAVE. Однако при ближайшем рассмотрении это оказывается совсем не так. Хотя по насыщенности математическими функциями FreePascal и уступает MATLAB'у, но это касается лишь функций высшего уровня. На среднем же уровне у FreePascal есть практически всё необходимое. Даже в стандартном составе FCL есть как отдельные среднеуровневые математические функции, так и небольшая математическая библиотека. И если этого не хватит, то в сети можно найти несколько отличных математических библиотек, которые написаны с использованием паскалевского кода.
3. Исследуем FCL
3.1 ucomplex.pp. Работа с комплексными числами
Здесь комплексное число представлено вполне в традиционной форме:
complex_single = record re: Real; im: Real; end;
Тип Real в зависимости от платформы будет выдаваться:
- в 32-ух битных системах как Single;
- в 64-ёх битных как Double.
Определены основные арифметические операции: :=, +, -, *, /, **. Операция := присваивает только реальную часть числа. Если нужно присваивание обеих частей числа, то нужно воспользоваться функцией init(). Есть операция сравнения. Эти операции можно проводить как с двумя комплексными числами, так и с одним комплексным и одним числом типа Real.
Определён основной набор элементарных математических функций:
- модуль, аргумент и обратное значение числа (cmod(), carg(), cinv());
- экспонента, натуральный логарифм, квадрат и квадратный корень (cexp(), cln(), csqr(), csqrt());
- косинус, синус, тангенс (ccos(), csin(), ctg());
- арккосинус, арксинус, арктангенс (carc_cos(), carc_sin(), carc_tg());
- гиперболические косинус, синус, тангенс (cch(), csh(), cth());
- гиперболические арккосинус, арксинус, врктангенс (carc_ch(), carc_sh(), carc_th());
- вывод числа в строковом виде (cstr()).
Ещё один модуль для работы с комплексными числами есть в библиотеке NumLib, однако там организация чисел принципиально другая - они представлены в виде объектов TP 5.5 (Object).
3.2 Шифрование и прочие шпионские штучки
- base-fcl/asci85.pp - так же известен как "Base85". Способ кодирования очень похож на Base64, но говорят, что работает быстрее;
- base-fcl/base64.pp - применяется в кодировании текстов писем;
- base-fcl/blowfish.pp - алгоритм с переменной длиной ключа. Основан на операциях XOR, поэтому работает быстро;
- hash/crc.pas - вычисление CRC[32|64|128]. Если нужно вычислить CRC16, то можно заглянуть в JclMath [1]
- hash/hmac.pp - два алгоритма: HMAC-MD5 и HMAC-SHA1. Использует для своей работы модули sha1.pas и md5.pas;
- hash/md5.pp - алгоритмы MD2, MD4 и MD5;
- hash/ntlm.pas - генерирует хэши сетевой аутентификации для старых Windows. Использует для своей работы модуль md5.pas. Содержит функции:
- LMGenerate - для систем на основе LanMan (типа Win3.1\Win95\Win98);
- NTGenerate - для системы WinNT.
- hash/sha1.pp - алгоритм SHA1
- hash/unixcrypt.pas - шифрование (а так же проверка правильности хэша) паролей для UNIX.
3.3 gmp.pas. Библиотека для работы с очень большими числами
Этот модуль является интерфейсом над сишной библиотекой GMP [2]. В Wiki Freepascal есть небольшая статейка по этому модулю, но она настолько краткая, что вряд ли даст понятие как с этим модулем работать. Это, скорее, просто новость, что "у нас теперь есть и это".
Если коротко, то стандартные типы данных имеют ограничение как на величину обрабатываемых чисел, так и (а это уже намного хуже) на длину мантиссы. Последнее влияет на точность вычислений. Библиотека GMP в принципе позволяет эту проблему решить за счёт самостоятельного определения программистом необходимой ему длины мантиссы. Теоретически её длина ограничивается только имеющейся в компьютере оперативной памятью, т.к. память под число выделяется динамически.
Библиотека работает с тремя типами данных:
- mpz_t - целочисленный;
- mpq_t - обыкновенная дробь. В ней числитель и знаменатель представлены типами mpz_t;
- mpf_t - дробь с плавающей точкой. Если вы работаете только с десятичными числами этот тип спокойно можно называть десятичной дробью.
Все типы являются составными, типа record. В них отдельными полями лежит служебная информация о числе и динамическое хранилище под само число. Перед использованием таких чисел их надо инициализировать, чтобы для хранилища был выделен какой-нибудь объём памяти. Что интересно, для целых чисел (и, естественно, обыкновенных дробей) память при нехватке перевыделяется. Для типа десятичной дроби такого уже не делается. Сколько выделено, столько и остаётся. Но если памяти не хватает, то её можно перевыделить вручную.
Математика для этого модуля определена скудновато, только самое необходимое - арифметические операции, некоторые дополнительные функции, генерация псевдослучайных чисел. Т.е. до стандартного паскалевского модуля MATH этот модуль сильно не дотягивает.
Все арифметические операции для этих типов чисел представлены в виде функций. При этом программирование становится довольно нудным, однако в Паскале, в отличие от Си, можно запросто определить арифметические операции для любых нестандартных типов данных. И таким образом написание программ с длинными числами значительно упростится.
Программа будет выглядеть примерно так:
program test_gmp;
Uses gmp;
Var
a, b, c: mpf_t;
Begin
// Определяем размер хранилища для числа по умолчанию
mpf_set_default_prec(128);
// Инициализация переменных
// (выделение памяти для хралища)
mpf_init(a);
mpf_init(b);
mpf_init(c);
// Присвоение числа из строки
mpf_set_str(a, '1111111111.1111111111', 10);
mpf_set_str(b, '2222222222.2222222222', 10);
// Сложение
mpf_add(c, a, b);
// Вывод результата на экран
mp_printf('Сумма чисел: %26.10Ff'#10, @c);
//Вычитание
mpf_sub(c, b, a);
// Вывод результата на экран
mp_printf('Разность чисел: %26.10Ff'#10, @c);
// очистка переменных
// (забираем у них память)
mpf_clear(a);
mpf_clear(b);
mpf_clear(c);
End.
Пояснения к коду:
- В первую очередь нужно определиться с размером хранилища чисел по умолчанию. Это актуально только для типа с плавающей точкой, т.к. целочисленный тип перевыделять память пожет автоматически. Размер хранилища определяется в битах. Теоретически никаких ограничений не существует, однако при инициализации переменной размер хранилища будет подкорректировано до числа кратному 32 (для 32-ухбитных компиляторов) или 64 (для 64-ёхбитных компиляторов). Поэтому лучше сразу задать верное значение. Величина хранилища вычисляется по формуле:
Количество_битов = ceil(количество_разрядов_мантиссы / log10(2)) - Далее, необходимо инициализировать все длинночисленные переменные, чтобы ихним хранилищам выделилась память.
- Начальное присвоение значений переменным в принципе можно делать из любого стандартного типа, однако для нецелых чисел лучше это делать в строковом виде. Тогда будет гарантией, что вы передали переменной верное значение.
- Все операции с числами делаются с помощью функций, которые состоят из префикса, основного названия и постфикса. Префикс определяет, какой тип чисел обрабатывается:
- mpz_ - целочисленный;
- mpq_ - обыкновенные дроби;
- mpf_ - с плавающей точкой.
- Вывод на экран осуществляется сиобразной форматирующей функцией. Паскалевский вывод работать не будет. Однако если преобразовать число в строку (PChar), тогда можно будет делать вывод и с помощью Write\WriteLn. Форматировать вывод в mp_printf() можно такой конструкцией:
%nn.mmFfЗдесь:- nn - общее количество цифр в числе;
- mm - цифр после запятой;
- F - тип длинного числа:
- F - число с плавающей точкой;
- Z - целое число;
- Q - обычная дробь.
- f - сишный тип числа, который будет на экране:
- E - нецелое число, научное представление (1.5634E-42);
- f - нецелое число с плавающей точкой (15211.45);
- d - десятичное целое число со знаком;
- u - тоже, но без знака.
- После того, как закончены все вычисления с длинными числами, необходимо забрать у них выделенную для хранилища память.
Более подробно о работе с длинными числами с помощью этой библиотеки можно почитать на нашем сайте [4].
3.4 fftw_s.pas. Быстрое преобразование Фурье (БПФ)
БПФ обычно все связывают с цифровым звуком. Однако сам маэстро Фурье изобрёл эту штуку для расчётов теплопроводности, так что есть мнение, что БПФ можно использовать где угодно. Естественно во времена Фурье ничего "быстрого" не существовало. Видимо тогда в уме и на бумажке эту функцию считали намного быстрее, чем сегодня на компьютере.
Модуль fftw_s является заголовочным файлом для библиотеки FFTW [5]. Правда в нём представлена не вся библиотека, а только самая минимальная часть:
- complex_single - тип данных, ячейка для массива сигнала комплексного типа;
- fftw_plan_dft_[1d|2d|3d] - соответственно если сигнал представлен одномерным, двумерным или трёхмерным массивом;
- fftw_plan_dft - эта функция на тот случай, если размерность массива превышает 3;
- fftw_execute - функция вычисления прямого или обратного БПФ. Параметр для прямого или обратного преобразования задаётся в предыдущей функции;
- fftw_destroy_plan - функция удаления плана;
- fftw_getmem\fftw_freemem - функции, которые выделяют или очищают память для массива сигнала.
Типы данных комплексные. Поля комплексного типа представлены типом Single. В принципе, нет никаких проблем поменять Single на Double. Для этого придётся в модуле fftw_s нужно поменять имя библиотеки с fftw3f на fftw3l и переопределить там же тип для ячейки массива.
В модуле ячейка объявлена таким образом:
complex_single = record re, im: Single; end;
Вычисление БПФ полностью представлена в прилагаемом в комплекте к модулю example.pas. Единственное что там плохо - нет ни одного комментария. Приведу его текст здесь со своими комментариями. Но сначала рисунок для большей понятности. На рис. 1 представлено преобразование аналогового сигнала в цифровую форму.
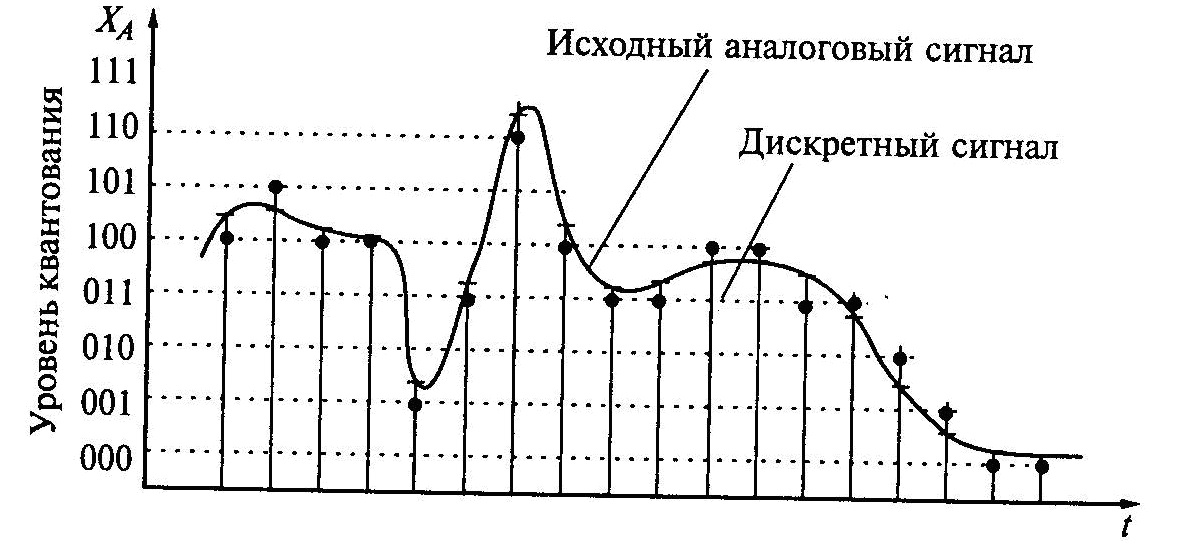
Рисунок 1. Представление аналогового сигнала в цифровой форме
На рисунке вы можете заметить, что уровень квантования проскакивает мимо реальной амплитуды сигнала. Это всего-лишь трёхбитовый пример, а в реальных устройствах количество бит не менее 8-ми. В высококачественных может быть и 16 и 24 бита. Т.е. уровень сигнала будет равен или максимально приближен к аналоговому оригиналу.
Всё время (T) периода сигнала происходит измерение его амплитуды. На рисунке эти измерения представлены вертикальными линиями перпендикулярными оси t. Для БПФ нас будет интересовать количество и, естественно, уровень сигнала этих измерений. Код примера:
program example;
Uses fftw_s;
Const
s=128; // Количество измерений сигнала
Var
i,o: Pcomplex_single; // Cигнал и его изображение после БПФ
// (одномерные массивы)
p: fftw_plan_single; // План вычисления БПФ
a: Cardinal;
Begin
// Выделение памяти для массивов значений
fftw_getmem(i, s*SizeOf(complex_single));
fftw_getmem(o, s*SizeOf(complex_single));
// Вычисление плана БПФ
// Параметры:
// s - количество измерений;
// i - сигнал;
// o - его изображение;
// fftw_forward - прямое преобразование;
// [fftw_estimate] - набор флагов.
p:=fftw_plan_dft_1d(s, i, o, fftw_forward, [fftw_estimate]);
// Значения амплитуды сигнала
For a:=0 To s-1 Do
Begin
i[a].re:=(Single(a)-64);
i[a].im:=0;
End;
WriteLn('Сигнал:');
For a:=0 To s-1 Do
WriteLn('(',i[a].re:8:4,',',i[a].im:8:4,')');
// Выполнение БПФ
fftw_execute(p);
WriteLn('Изображение сигнала после БПФ:');
For a:=0 To s-1 Do
WriteLn('(',o[a].re:8:4,',',o[a].im:8:4,')');
// Удаление плана
fftw_destroy_plan(p);
// освобождение памяти
fftw_freemem(i);
fftw_freemem(o);
End.
Если Вы не хотите пользоваться сишной библиотекой, то для БПФ можно использовать код из статьи на нашем сайте [8].
3.4 NumLib - cерьёзная математика
Это большой, хотя и неполный набор математических функций среднего уровня. Первоначально код функций писался на языке Алгол-60 в начале 60-ых годов прошлого века в нидерландском техническом университете города Эйндховена. Впоследствии код был переведён на Паскаль, т.к. эти языки очень похожи. Для функций есть неплохая документация [9], правда она неполная. К сожалению примеров довольно мало.
Список модулей и функции, которые они выполняют:
- spe - специальные функции;
- sle - решение систем линейных уравнений (СЛАУ);
- roo - нахождение корней уравнений;
- int - интегрирование;
- ode - решение обыкновенных дифференциальные уравнений;
- ipf - интерполяция и прогнозирование продолжения кривых;
- omv - основные операции с матрицами и векторами;
- iom - операции ввода-вывода матриц и векторов;
- inv - обращение матрицы;
- det - определители матрицы;
- eig - собственные значения.
Не хватает одной существенной области - нет функций оптимизации.
Функции используют собственные типы данных:
- ArbInt - целочисленный, который является аналогом LongInt;
- ArbFloat - с плавающей точкой, который зависит от объявления макроса ArbExtended:
- Extended - если макрос объявлен (объявлен по умолчанию);
- Double - если макрос не объявлен.
Несколько запутывает ситуацию то, что в заголовках всех функций эти типы используются не по прямому, так сказать, назначению, а почему-то как указатель на массив, что не сильно соответствует паскалевскому стилю работы с массивами. Точнее, здесь это первый элемент массива. Видимо в начале 60-ых для Апгола это было самое правильное решение.
Таким образом, в большинстве случаев встречая функцию типа:
Умножение(a, b: ArbFloat; n: ArbInt): ArbFloat;;
Речь идёт об умножении матрицы на матрицу или матрицы на вектор, или вектора на вектор, количество ячеек которых равно n. Здесь a и b - это первый элемент массива или вектора и сильно напоминает ссылку. Впрочем, определить матрица задана или вектор можно по количеству параметров, которые задают размер и помещаются после ссылки на матрицу или вектор. Если параметр один - это будет вектор, если два - это матрица. Таким образом в вышеприведённой функции речь идёт о векторах. В реализации функции будет что-то типа такого:
Умножение(a, b: ArbFloat; n: ArbInt): ArbFloat;
Const
highestelement=20000;
Type
TVector = array[1..highestelement] of ArbFloat;
Var
v1, v2: ^TVector;
i: ArbInt;
Begin
v1:=@a;
v2:=@b;
Умножение:=0;
For i:=1 To n Do
Умножение := Умножение+v1^[i]*v2^[i]
End;
Здесь необходимо небольшое пояснение. Внутри функций библиотеки, массивы представлены именно так - с явно заданным количеством ячеек. Это может показаться странным, но не стоит забывать, что функции писались довольно давно, когда динамических массивов в Паскале ещё не было. И, как минимум, с 2000 года код не изменялся. Поэтому если будете работать с этой библиотекой, помните про размер массивов.
Таким образом, программа, которая использует подобную функцию будет выглядеть примерно так:
program TestNumLib;
Uses numlib;
Const
n = 3;
Var
a: array[1..n] of ArbFloat;
b: array[1..n] of ArbFloat;
AlgProd: ArbFloat;
Begin
a[1] := 1.0;
a[2] := 2.0;
a[3] := 3.0;
b[1] := 4.0;
b[2] := 5.0;
b[3] := 6.0;
AlgProd := Умножение(a[1], b[1], n);
WriteLn('Алгебраическое умножение векторов a и b:');
WriteLn(AlgProd);
End.
В NumLib функция умножения векторов называется omvinp().
4. Сторонние библиотеки
4.1 Старинные, но работающие библиотеки
4.1.1 Turbo Pascal Numerical Methods Toolbox
Исторически, это первая математическая библиотека среднего уровня, которая появилась в 1986 году для Turbo Pascal 3 (архив [21]). Использовать её можно, но с некоторой осторожностью, обязательно посмотрев исходники и, если нужно, подредактировать их. По крайней мере из исходников обязательно нужно удалить зависимости от модулей Dos и Crt. Они там точно не нужны.
По функционалу эта библиотека немного превосходит NumLib и, что особенно приятно, использует традиционные для Паскаля (и для математики) массивы, которые начинаются с 1. Динамических массивов так же нет и их размер обычно ограничивается какой-либо константой. Это нужно иметь в виду. Для чисел с плавающей точкой используется тип Float, который объявлен как Double. Это позволяет надеяться на более точные результаты. Есть хорошая документация в виде книжки. Лицензия на эту библиотеку для сегодняшнего времени неясна, но в силу своей устарелости вряд ли правообладателю придёт в голову судиться за незаконное использование.
Функционал по главам книги:
- Глава 2. Корни уравнений одной переменной
- Глава 3. Интерполяция
- Глава 4. Дифференцирование
- Глава 5. Интегрирование
- Глава 6. Операции с матрицами (в том числе решение СЛАУ)
- Глава 7. Собственные значения
- Глава 8. ОДУ (в основном методы Рунге-Кутта, но попадается и Адамс)
- Глава 9. Аппроксимация методом наименьших квадратов
- Глава 10. БПФ
- Глава 11. Графические программы
К последней главе следует подходить с особой осторожностью, поскольку ни в Windows, ни в Unix досовские рисовалки вряд ли будут работать. Ещё пуще внимания следует уделить каталогам ASM\OBJ, поскольку там содержаться подпрограммы работы со стеком. В каталоге ASM - исходный код этих программ. В их заголовках написано, где они используются. Я бы советовал пересмотреть коды упоминаемых в заголовках программ и исключить ассемблерный код. Если же вы непременно захотите его использовать, то лучше всего будет эти asm'ки переписать под 32- и 64-битный ассемблер. Впрочем, я не большой специалист по ассемблеру, возможно исходный код и так будет работать. Однако имейте в виду.
Таким образом использование этой библиотеки исключительно на ваше усмотрение. В любом случае, прежде чем брать оттуда ту или иную функцию в рабочий проект, следует её тщательно проверить на тестовых данных. Не забывайте, что судя по дате выпуска эта библиотека разрабатывалась для TurboPascal 3.0, а с тех пор много воды утекло.
4.1.2 Библиотека численного анализа НИВЦ МГУ
Эта библиотека [10] родилась довольно давно, как набор математических функций для языка Фортран. Когда язык Pascal и, в частности, Object Pascal, набрал популярность, была сделана версия библиотеки и для него с помощью программного конвертора FORPAS [11]. Несколько печалит то, что фортрановские алгоримы были преобразованы "в лоб", поэтому в программы перекочевали и жившие тогда в фортраньем коде GOTO.
Использование кода из библиотеки для некоммерческих целей свободное.
Функционал:
- Простейшие вычислительные операции;
- Элементарные статистики, обработка данных;
- Статистические критерии;
- Алгебра полиномов;
- Линейная алгебра;
- Специальные функции;
- Численное интегрирование;
- Обыкновенные дифференциальные уравнения;
- Интерполяция, аппроксимация, сглаживание, численное дифференцирование;
- Анализ и синтез рядов. Быстрые преобразования;
- Решение уравнений и систем общего вида;
- Математическое программирование;
- Интегральные уравнения;
- Генерация случайных чисел.
В этой библиотеки самое привлекательное - описание всех функций на русском языке. Каждая функция на отдельной страничке. Описание подробное, но без излишнего уклона в математику. Для каждой функции есть пример и тестовые данные с правильным ответом. Это на тот случай, если вы соберётесь функцию переделывать. А переделывать придётся, если вы студент и захотите предъявить её преподавателю как реализацию своего замысла. Потому что придётся избавляться от GOTO, иначе никто не поверит, что это ваше.
Ещё одно достоинство - в отличие от предыдущей версии эта библиотека была рассчитана на работу вместе с Delphi, следовательно код не является старым и его работоспособность очень близка к 100%. К "старым библиотекам" я её отнёс исключительно потому, что паскалевский код транслировался со старого Фортрана. К сожалению "осовремениванием" библиотеки никто не занимается, поэтому исходники лучше всего использовать творчески, т.е. делать на их основе свои функции.
4.1.3 Numerical Recipes
В том же 1986 году, что и "Turbo Pascal Numerical Methods Toolbox", группой преподавателей Кембриджского университета была выпущена отличная книга по численным методам "Numerical Recipes: The Art of Scientific Computing" [12] с иллюстрацией этих методов кодом на языке Fortran, естественно старом. Поскольку языки Fortran и Pascal довольно похожи, особенно в плане использования массивов, примерно к 1990 году был выпущен репринт этой книги с иллюстрациями кодом на языке Pascal. Название "Numerical Recipes in Pascal: The Art of Scientific Computing". К сожалению, для текущего (третьего) издания, исходный код доступен только за плату ($70), однако в сети доступен код первого издания (архив [22]) в котором написано, что
** Do I really get this whole library for FREE? ** Yes, providing that you follow these simple rules: (1) You must read and accept the disclaimer of warranty at the end of this document. (2) You must not expect any user support from Numerical Recipes Software, Cambridge University Press, or the authors of the Numerical Recipes books. (3) You must not copy or redistribute any of the programs or procedures for commercial purposes. You CAN make copies of the programs for your friends and colleagues, providing that you include this file (especially its copyright notice and disclaimer of warranty) with any copy that you make.
Таким образом для некоммерческого применения этот код свободно можно использовать а так же копировать в любое нужное вам место. К сожалению самой книжки в открытом доступе я не нашёл.
Поскольку паскалевский код переведён со старого Фортрана, в коде присутствует довольно много GOTO. Работе программ это нисколько не мешает, однако если вы студент и понесёте этот код своему преподавателю, пытаясь выдать за творение собственного гениального разума, то разоблачат вас практически сразу же. Поэтому стоит потратить некоторое время на изменение кода, чтобы убрать оттуда те самые пресловутые GOTO. Это будет крайне полезно для вас, как для программиста.
В библиотеке содержится около 200 функций, с примерами к каждой функции. Примеры имеют расширение .DEM. Каждая функция представлена в отдельном файле, поэтому её можно либо скопипастить в свой код, либо подключить с помощью директивы {$I ФайлСФункцией.PAS }. В каждом файле-функции, в заголовке содержится её краткое описание. Комментарии в коде отсутствуют, поэтому желательно скачать из сети книжку, чтобы в трудных и непонятных случаях ориентироваться по ней.
Динамические массивы отсутствуют, поэтому код потребует адаптации к вашей программе в плане размеров массивов. Типы данных представлены типом Real, поэтому в 64-ёхбитной системе их можно не менять, а вот в 32-ух желательно или поменять на Double, либо переобъявить тип Real как Double. Это благотворно повлияет на точность результата.
Функционал:
- Практически все популярные способы решения СЛАУ, а так же определитель и инверсия матриц;
- Интерполяция и экстраполяция;
- Интегрирование;
- Оценка последствий решения функции;
- Специальные функции;
- Получение псевдослучайных чисел;
- Сортировка;
- Поиск корней и нелинейные функции;
- Минимум\максимум функций;
- Получение собственного значения;
- Преобразование Фурье;
- Статистическая обработка данных;
- Моделирование;
- Решение обыкновенных дифференциальных уравнений;
- Двухточечные краевые задачи;
- Дифференциальные уравнения в частных производных.
Как и в случае с "Turbo Pascal Numerical Methods Toolbox" к коду следует подходить осторожно. Код не привязывался к конкретному компилятору языка, а скорее всего рассчитывался на существовавший тогда стандарт. Об этом говорит присутствующие во всех демонстрашках параметры главной программы (input, outpu). Это можно спокойно стереть или не обращать внимания. Поскольку документация к коду отсутствует, только-только начинающим программистам использовать его будет трудновато.
4.1.4 Numerical methods
Ещё одна книга, аналогичная по тематике предыдущей, которую написал профессор Калифорнийского университета Джон Мэтьюз "Numerical methods for Mathematics, Science and Engineering". Код примеров [23] более современный, т.к. базируется на втором издании книги, которая вышла в 1992 году. По крайней мере, GOTO в коде совсем чуть-чуть, хотя код, так же как и в предыдущем случае, переделывался из FORTRAN. Исходный код библиотеки так же является свободным:
This free software is complements of the author. It is permissible to copy this software for educational purposes, provided that it is used with the textbook. The software may not be sold for profit and may only be sold in such a way that the cost of reproduction are recovered.
В интернете эту книгу (а так же и код) оценивают как более продвинутую, поскольку автор не был поставлен в условия экономии места на странице, в отличие от предыдущих авторов. Код организован по другому - все функции встроены в файлы примеров, поэтому код примеров имеет законченный вид. Этот момент очень удобен для студентов. Заголовки файлов содержат описание, что именно рассчитывается. К сожалению комментариев в коде исчезающе малое количество. В большинстве случаев программы интерактивны, т.е. требуют после запуска выбора какого-то пункта для исполнения и ввода необходимых параметров. Динамические массивы не применяются.
Функционал:
- CHAP_2. Решение нелинейных уравнений f(x) = 0
- CHAP_3. Решение СЛАУ AX = B
- CHAP_4. Интерполяция и полиноминальная аппроксимация
- CHAP_5. Продолжение кривых
- CHAP_6. Дифференцирование
- CHAP_7. Интегрирование
- CHAP_8. Оптимизация
- CHAP_9. Решение ОДУ
- CHAP_10. Решение ОДУ в частных производных
- CHAP_11. Собственные значения
Эта библиотека прекрасно подходит для обучения численным методам. Переделки будут минимальны. Во многих случаях достаточно будет просто русифицировать все строки, которые выводит программа на экран. Для научного применения код нужно тщательно просматривать и переделывать под себя, под свою задачу. Книгу в свободном доступе я не нашёл, поэтому совсем начинающим программистам так же будет трудновато её использовать, как и предыдущую библиотеку.
4.1.5 Compact numerical methods for computers. Linear algebra and function minimisation
Это несколько менее фундаментальная книга по численным методам, чем две предыдущих, о чём свидетельствует её название. Тем не менее так же является весьма интересной в плане решения уравнений линейной алгебры и методов оптимизации. Описание там весьма подробное и понятное.
В отличие от предыдущей книги, коды примеров изначально создавались именно для языка Pascal и компилятора TurboPascal. В первой главе написано, что код рассчитан на тогдашние персональные компьютеры, которые имели весьма ограниченные ресурсы. Архив с кодом [24].
Названия файлов в архиве строятся по такому принципу:
- alg??.pas - примеры в книге. Здесь ?? - это номер алгоритма из книги. Например, alg01.pas соответствует Algorithm 1 в книге. И так далее;
- dr*.pas - это программы-примеры для соответствующего алгоритма. Все примеры очень подробно прокомментированы;
- ex*.cnm - это файлы с данными к кодам примеров;
- Все остальные файлы содержат либо включаемый код, либо какое-то описание. Включаемый код нужно обязательно просмотреть, т.к. он предназначался для очень старого Паскаля, наверняка там нужно что-нибудь изменить.
Функционал:
- Алгоритмы с 1 по 16 - линейная алгебра;
- Алгоритмы с 17 по 25 - минимизация.
Прекрасно подходит для изучения численных методов линейной алгебры и методов оптимизации. Рекомендуется в том числе и начинающим. Однако к коду необходимо подходить осторожно из-за его привязки к очень древнему TurboPascal. Необходима тщательная проверка тестовыми данными.
4.2 Современные библиотеки
4.2.1 tpmath\dmath\lmath - три имени одной библиотеки
На самом деле это одна и та же библиотека, написанная когда-то заведующим фармакологической лабораторией медицинского факультета университета Лимож (Франция), доктором Жаном Дебо. К сожалению, примерно с 2012 года эту библиотеку больше никто не разрабатывает, однако то что есть работает вполне прилично, в том числе и в FreePascal. Кстати, возможность работы в FreePascal специально упомянуто автором в документации. которая идёт в комплекте. В интернете довольно легко найти примеры, которые используют эту библиотеку.
Первая версия разрабатывалась для Turbo Pascal (отсюда и одно из названий - tpmath). В дальнейшем библиотека переделывалась и дорабатывалась под Delphi (dmath). Последнее название (lmath [13]) - это просто распределение отдельных модулей по каталогам в зависимости от того, какую именно проблему решает тот или иной модуль. Как раз последнюю исследовать более удобно, чтобы не отвлекаться на неинтересные, в данный момент, направления.
Математика в библиотеке строится на типа Float, который, в свою очередь, определяется заданием макроса для компилятора:
- SINGLEREAL - Float имеет тип Single;
- DOUBLEREAL - Float имеет тип Double;
- EXTENDEDREAL - Float имеет тип Extended.
Как и в многих других библиотеках, здесь имеются почти все популярные константы для того, чтобы сократить время вычислений. Тип Complex имеет традиционное строение - в виде Record. Дополнительно в типах заданы различные виды векторов и матриц на основе безразмерного массива.
В архиве LMath [25] каталоги с модулями имеют такие назначения:
- UGenMath - в большей степени для элементарной математики. Однако здесь лежат модули определяющие базовые типы:
- utypes.pas - определён тип Float, вектора, матрицы и константы, а так же элементарные функции по работе с ними. Так же здесь определён тип complex;
- ucomplex.pas - здесь определены арифметические операции по работе с комплексными числами, а так же элементарные математические функции по работе с ними.
- UIntegrals - интегрирование методом Гаусса-Лежандра, методом трапеций, а так же решение диффуравнений методом Рунге-Кутта-Фельберга четвёртого порядка с адаптивным подбором шага интегрирования;
- ULineAlgebra - функции линейной алгебры, например, решение СЛАУ методом Гаусса-Жордана или LU-разложения, поиск собственных значений и т.п.;
- UMathStat - уравнения математической статистики, например, дисперсионный анализ, биноминальное распределение и т.п.;
- UMathUtils - кое-какие вспомогательные утилиты, например, сортировка или поиск строк по двоичному дереву;
- UNonLinEq - решение нелинейных уравнений;
- UOptimum - методы оптимизации нескольких переменных, в том числе и сложные, например, генетический алгоритм;
- UPlotter - рисование. Применительно к кроссплатформенности или написанию научного труда, представляет интерес только один модуль - utexplot.pas, который делает рисунки для LaTeX. Остальные модули - для Dos и Windows;
- UPolinoms - работа с полиномами, а так же решение квадратных, кубических и четвёртой степени уравнений;
- URandoms - разные методы получения псевдослучайных чисел;
- URegression - регрессионный анализ, пригодится для обработки результатов экспериментов. Так же здесь можно найти Быстрое Преобразование Фурье (БПФ);
- USpecRegress - аналогично предыдущему, содержит более "изощрённые" функции.
Подходит для обучения, т.к. есть исходники и документация к функциям. Библиотека давно не обновляется и, похоже, автором заброшена. Для учёного применения использовать осторожно, т.к. есть некоторые функции, которые при определённых условиях вылетают. Исследование кода некоторых из них показало, что это не ошибки как таковые, а скорее лишний функционал, который автору может быть и был нужен, но при некоторых входных условиях он может давать вылет программы.
4.2.2 Alglib - с миру по нитке
Несмотря на своё название - Alglib - это не сборник алгоритмов. Начинался проект [14] как сборник программ, которые решают ту или иную конкретную математическую проблему. Начинали это дело русские программисты, но постепенно проект вышел на международный уровень. На сегодняшний день это большая откомпилированная библиотека разнообразнейших функций, для которой имеются интерфейсные модули для нескольких языков программирования, в том числе и для Delphi. Это запросто позволяет подключать библиотеку к программам на FreePascal. В архиве [15] содержится библиотеки для Windows и Linux, 32-ух и 64-ёх разрядные реализации. Для Linux только 64-ёх разрядная. Существуют две версии:
- ALGLIB Commercial Edition - коммерческая;
- ALGLIB Free Edition - свободная.
Свободная версия отличается от коммерческой несколько меньшим уровнем оптимизации и отсутствием возможности работать в многопоточном или многопроцессном режиме. Функционал по алгоритмам у обеих версий один и тот же. В коммерческой версии присутствует техподдержка.
Функционал:
- Решение уравнений на основе плотных и разреженых матриц;
- Различные операции с матрицами, например, умножение, LU-разложение, инверсия и т.п.;
- Собственные значения;
- Интерполяция;
- Оптимизация (нелинейная, квадратичная, с уловиями, без условий...);
- БПФ, свёртка, корреляция;
- Анализ данных (классификация, регрессия и т.п.);
- Анализ временных рядов;
- Статистика: основные алгоритмы
- Проверка гипотез;
- Специальные функции;
- Интегрирование;
- Нелинейные и полиномиальные уравнения;
- Дивверенциальные уравнения;
- Всякое другое...
В архиве есть краткий справочник по функциям применительно к их работе в Delphi. Самая функционально насыщеная и быстроработающая в FreePascal библиотека. Не подходит для обучения, т.к. нет исходников. Правда в сети можно найти старые исходники, но они сильно давнишние. Больше подходит для учёного применения, т.к. работает быстро. Библиотека регулярно обновляется.
4.2.3 Wolfgang Ehrhardt
Это не название библиотеки, а человек, который разработал и собрал несколько очень интересных математических комплектов [17]. Этот проект довольно давнишний и в некоторых модулях написано, что они могут работать даже в BP\TP 7. В Delphi - само собой разумеется, так что и в FreePascal будут работать, поскольку в них не предполагается использование каких-либо ОС-зависимых компонентов.
Самое интересное - математические сборки:
- AMath\DAMath - набор как элементарных, так и среднеуровневых функций. Сборки позиционируются как особоточные. Ещё одна в высшей степени интересная особенность - наличие комплексных типов и чисел с плавающей точкой в 16 байт (double double). Ну и напоследок - возможность работы с кватернионными типами, т.е. векторами в четырёх измерениях. DAMath отличается тем, что вся математика у него строится на типе Double. У AMath - на типе Extended;
- MPArith - арифметика, низкоуровневые и некоторые среднеуровневые функции по работе с числами, разрядность которых ограничена только величиной вашей оперативной памяти (multiprecision). Аналог связки сишных библиотек GMP, MPFR и MPC;
Второе, не менее интересное направление - CRC\Hash\Crypto. По CRC, в отличие от FCL'евского модуля, можно вычислять CRC16\24\32\64. CRC128 нет, но возможно оно и не очень востребовано. По крайней мере Википедия пишет, что вместо него используют криптографические хэш-функции. Большое количество хэш-функций и разных алгоритмов шифрования. Российских стандартов к сожалению нет.
В архивах приложены текстовые файлы со списком имеющихся функций и кратким пояснением, что эта функция делает. В исходных кодах так же заголовок каждой функции прокомментирован описанием. Подходит как для обучения, так и для учёного применения. Функционал скорее можно назвать низкоуровневым, чем среднеуровневым. Однако по сравнению со стандартным модулем "Math" низкоуровневых функций прямо-таки завались. Это просто сказка, а не библиотека. На все случаи жизни.
Библиотека регулярно обновляется.
5. Какую библиотеку выбрать?
Откровенно говоря, именно в таком ключе вопрос ставить не стоит. Выбор всегда обусловлен поставленной задачей. Поскольку все библиотеки (кроме одной) представлены в виде исходников, я бы покопался в них всех и понадёргал бы функций которые мне понравились и которые, самое важное, мне понятны. В табл. 1 кратко представлены общие впечатления от библиотек по двум, так сказать, номинациям:
- Для учебных целей. Здесь главная задача это повышенная наглядность и понятность текстов функций;
- Для прочего, например, научного употребления. В этом случае наглядность следует применять скорее для заголовков файлов и функций, чем для их содержимого. В отличие от предыдущего случая здесь необходима быстрота принятия решения по поводу использовать ли функцию или искать дальше. И, несомненно, наличие документации.
В таблице сравниваются только те библиотеки, которые имеют более-менее разнообразный функционал, т.е. универсальные библиотеки, а не те, которые направлены на решение одной или пары-тройки задач.
Таблица 1. Краткое сравнение библиотек
| Библиотека | Для учебных целей | Для прочего |
|---|---|---|
| Numlib | Не рекомендую из-за нетрадиционного использования массивов в заголовках функций. Это может вызвать непонятки не только у студента, но и у преподавателя, который проверяет код. Есть демонстрашки, но без комментариев и подписей, какая демо что демонстрирует. | На ваше усмотрение. Если вас не смущает ограничение на кол-во ячеек в массивах, используемых внутри функций, то проблем с их применением не будет. Документация неполная. |
| Turbo Pascal Numerical Methods Toolbox | На ваше усмотрение. Если собираетесь использовать, предварительно коды необходимо внимательно изучить, наверняка там есть что поправить. Есть книга. | На ваше усмотрение. |
| Numerical Recipes | Рекомендую. Но с обязательным предварительным изучением кода с целью удаления оттуда GOTO. Книга есть, но бесплатно найти её трудно. | Можно использовать. Только предварительно нужно переделать код для возможности использования безразмерных массивов, как это практикуется в современном Pascal. |
| Numerical methods | Рекомендую. Переделка кода требуется редко, но изучить его обязательно. В нём много строк на иностранном языке, желательно их сделать на русском. Книга есть, но бесплатно найти её трудно. | Можно использовать. Только предварительно нужно переделать код для возможности использования безразмерных массивов, как это практикуется в современном Pascal. |
| Compact numerical methods | Пожалуй наиболее интересная библиотека, т.к. код демонстрашек в ней подробно прокомментирован. Прилагаемая книжка достойна пристального внимания. | Если вам достаточно линейной алгебры и оптимизации, то хороший выбор. Код, как и в предыдущих библиотеках, лучше всего переделать под использование безразмерных массивов, где это необходимо. |
| lmath | Рекомендую. Есть и документация и исходники. Писал преподаватель для студентов. Документация хорошая, не перегруженная математикой, понятная. Есть демонстрашки. Все с подписями кто что делает. В кодах встречаются комментарии, но маловато. | Вполне можно использовать. Поиск нужной функции лёгок, т.к. есть хорошая, разбитая по разделам, документация в которой кратко и понятно описаны способы решения задачи, входные и выходные параметры. Исходник можно посмотреть и, если нужно, подправить. |
| Alglib | Не рекомендую из-за отсутствия исходников. На старых версиях сайта (которые при известном старании пока ещё можно найти в интернете) исходники были. Документация простая и понятная. Демонстрашек нет. | Вполне можно использовать, если только вас не смутит отсутствие
информации о том, как именно решается та или иная задача.
В документации, разбитой на разделы, есть описание заголовков функций для Delphi. В них:
|
| Wolfgang Ehrhardt | Можно использовать. В модулях есть подписи, для чего они служат. У каждой функции есть коммент, для чего функция предназначена. Кроме того, у всех архивов есть текстовые файлы со списком функций и кратким пояснением, для чего функция нужна. Демонстрашек нет, но есть тестовые файлы, которые могут послужить демонстрашками. | Можно использовать. Единственный недостаток - нет описаний для параметров функций. Документация очень краткая и уступает предыдущим библиотекам. |
Теперь поговорим о недостатках. А как же без них?
Самый наиглавнейший недостаток - не очень высокая, мягко говоря, скорость обработки больших массивов данных. Правда тут есть один нюанс. Для многомерных массивов скорость сильно зависит от порядка обработки размерностей. Это легко проверяется. Тем не менее, Pascal никогда не позиционировлся как компилятор для быстрых программ. Небольшая табличка с результатами тестов трёх разных библиотек (см. табл. 2) показывает скорость работы при решении СЛАУ (у нас всё как у взрослых - ТОП500 суперкомпьютеров тоже меряются "у кого больше" исключительно на СЛАУ). Сразу предупреждаю, сравнивать паскалевские программы с фортрановскими не стоит в принципе, т.к. Фортран до сих пор по скорости остаётся впереди планеты всей. Современный Си если ему и уступает, но не так уж и много, поэтому его из соревнований тоже исключаем. Интереснее всего будет померятся со специализированными математическими программами, типа MATLAB. Правда и здесь мы всё-равно будем мерятся либо с сишными, либо с фортрановскими двоичными библиотеками. Так что приготовьтесь к тому, результат будет немного печален.
MATLAB'а у меня нет и тратить деньги на его покупку что-то неохото. Поэтому меряться будем с аналогом MATLAB'а - GNU Octave и с набирающим популярность математическим пакетом Julia. Размерность матрицы для СЛАУ не сильно большая, 2000 х 2000, чтобы не уснуть в ожидании ответа.
Таблица 2. Скорость вычисления СЛАУ с помощью разных библиотек
| Библиотека | Откомпилировано без оптимизации | Откомпилировано с ключом -O2 |
|---|---|---|
| NumLib, сек. | 20,54 | 15,27 |
| Numerical methods, сек. | 23,30 | 18,07 |
| alglib, сек. | 3,40 | 3,30 |
| LMath, сек. | 79,15 | 39,28 |
| GNU Octave, сек. | 3,12 | - |
| Julia, сек. | 0,59 | - |
Вот так и выясняется, что в прошлом веке умели писать более быстрые программы, чем в веке нынешнем.
Большого смысла проверять все библиотеки на скорость нет. Я думаю этот пример показателен. Как видно, даже ключ оптимизации при компиляции не сильно помогает приблизится по скорости к математическим пакетам.
Хорошая скорость alglib понятна. В ней паскалевский код всего лишь интерфейс для уже готовой скомпилированной библиотеки. В многопоточном варианте, наверняка скорость будет ещё лучше.
Итак, если вам нужна скорость работы с большим оьъёмом данных, то альтернативы библиотеке alglib нет. Во всех остальных случаях, если объёмы данных небольшие, то принципиальной разницы в использовании той или иной библиотеки не будет.
Второй недостаток касается старых библиотек. В старом Паскале отсутствовала возможность применения динамических (безразмерных) массивов. Естественно их можно было делать как в Си, т.е. на основе указателей. Но в этом случае лучше перейти на язык Си, чтобы не путаться.
При попытке создать достаточно большой статический массив, когда используются старые библиотеки, мы с большой долей вероятности столкнёмся с ошибкой переполнения стека. При переделке функции\программы на динамический массив следует иметь в виду:
- В старых программах массивы начинались, как правило, с 1. Чтобы кардинально не переделывать алгоритм, под безразмерный массив для каждой размерности нужно выделять количество ячеек + 1. Таким образом, нулевая ячейка остаётся незадействована, но эта потеря не такая уж и существенная по сравнению с переделкой алгоритма;
- Про такие пустяки, как выделение памяти под динамический масив можно было бы и не упоминать, но, увы, слишком часто об этом забывают;
- Частенько можно встретить заполнение массива данными из файла. Почти в 100% случаев старые программы для этого используют текстовый файл. С большими массивами и чтение и запись в такие файлы будут происходить очень долго. Поэтому желательно текстовый файл поменять на типизированный. На скорости чтения\записи данных это скажется очень благоприятно.
В качестве примера переделки статического массива в динамический можно использовать тест из архива [26] для библиотеки "Numerical methods".
6. P.S. Внешние библиотеки. Зона особого внимания!
Если вам нужно решить какую-нибудь махонькую задачку типа СЛАУ, вовсе не обязательно подключать какой-либо громоздкий сторонний модуль или вставлять сторонний громоздкий кусок кода (а для СЛАУ он будет громоздким, не сомневайтесь). Можно, воспользовавшись идеей Alglib, взять какую-нибудь внешнюю двоичную математическую библиотеку, подготовить заголовок функции и, оп-ля, не парясь получть махонький код. Увы, с математикой есть большая опасность по незнанию её истории нарваться на изрядный казус.
Дело в том, что как раз в математике до сих бешеной популярностью пользуются фортрановские библиотеки, например BLAS или LAPACK. В интернете можно встретить парочку статеек о том, что Фортран хранит многомерные массивы по другому, не так как в Паскале или Си. Это так и есть: сначала подряд идут ячейки первой колонки, потом второй и так далее. См. рис. 2.
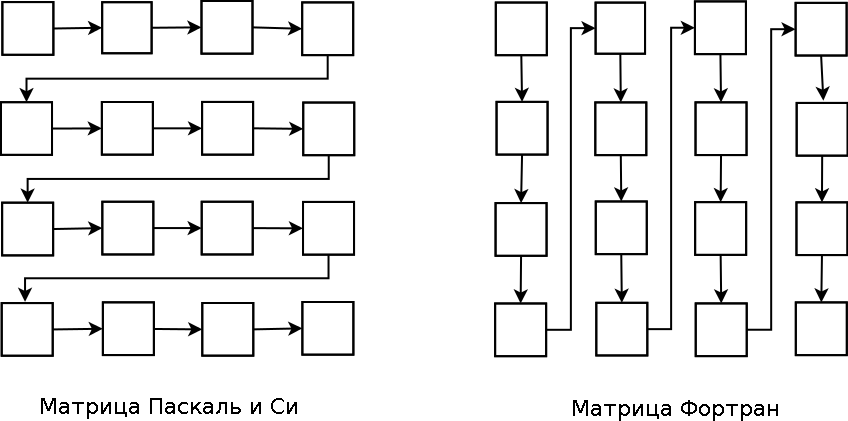
Рисунок 2. Расположение в памяти ячеек массива Паскаль\Си и Фортран
Однако если вы подумаете, что простым транспонированием, к примеру, матрицы можно легко решить проблему, как об этом пишут авторы статей, то вы ошиблись. После транспонирования правильный результат всё равно получить не удастся, хотя функция по внешним признакам отработает правильно, без ошибок. Ошибка выскочит уже при завершении программы, в том месте, где идёт работа оператора "End.".
Покапушки в исходном коде LAPACK выявило, что это проблема не только Паскаля, но и Си. В сишных заголовках к LAPACK я и выяснил метод исправления этой проблемы. В фортраньи функции\подпрограммы нужно передавать одномерный массив, составив его из многомерного, т.е. начало второй колонки добавляется к хвосту первой и так далее. Должно получиться как на рис.3.
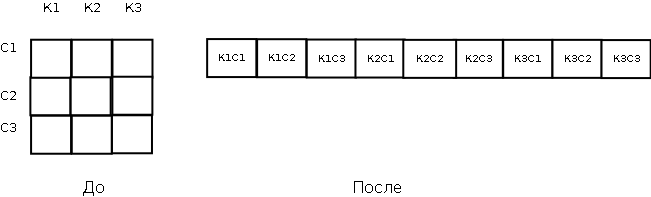
Рисунок 3. Одномерный массив после преобразования матрицы
Вторая особенность фортрановских функций\подпрограмм - параметры в них передаются исключительно в виде ссылки. Это делает Фортран самым быстрым вычислителем, по сравнению с другими языками-компиляторами. Вряд ли это стоит считать проблемой.
Таким образом, перед использованием функций из фортраньих библиотек и если есть необходимость использовать более чем одномерные массивы (как пример - матрицы) нужно выполнить такие шаги:
- Либо матрицу изначально заполнять по фортраньему принципу, т.е. сначала заполняется первая колонка, потом вторая и т.д., либо, если у вас уже есть готовая матрица (из Паскаля или Си), транспонировать её;
- Фортранью матрицу преобразовать в одномерный массив, т.е. к хвосту первого столбца присоединяется начало второго столбца и т.д. (см. рис.3);
- Передавать в фортранью функцию не массив, а указатель на первый элемент массива.
В архиве с примерами [26] есть файл "test_externlib.pas", который эти шаги демонстрирует.
Теперь ещё один очень важный момент. Многие могут подумать "ну, вот, сколько возни из-за одного простого действия. А стоит ли оно того?". Безусловно стоит. Смотрите в табл. 3.
Таблица 3. Скорость вычисления СЛАУ с помощью фортрановской библиотеки LAPACK
| Библиотека | Откомпилировано без оптимизации |
|---|---|
| LAPACK+BLAS, сек. | 3,07 |
| OpenBLAS, сек. | 0,86 |
Как видно, скорость вычисления выше, чем у Alglib, которая использует сишную библиотеку. В варианте LAPACK+BLAS скорость сравнима с GNU Octave, а в варианте с OpenBLAS (это LAPACK+BLAS в одном флаконе) сравнима даже с Julia. Таким образом, в случае нужды в скорости вычислений, такой вариант должен стоять на самом первом месте.
7. Заключение
Приведённый здесь список математических библиотек ни в коем случае не является исчерпывающим. В интернете для Pascal можно найти очень много. В своё время для Turbo Pascal было написано довольно много кода, в том числе как специализированных функций для одной задачи, так и многофункциональных библиотек. То что они для TP пускай вас не смущает. Обычно они рабочие, но предварительно просмотреть их нужно и, возможно, кое-что подправить, т.к. люди их писали под свои задачи, а вовсе не под ваши. В качестве примера можно привести математические подпрограммы из [18].
Ещё более интересна может быть книга [19], поскольку все примеры там очень подробно и понятно объяснены на русском языке. Математики самый минимум, без нудной теории. Описание даётся только в рамках практического применения программного кода. Скан книги без проблем можно найти в интернете. Я её настоятельно рекомендую, т.к. она очень хорошо помогает понять алгоритм расчёта той или иной функции. Единственный печальный момент, никто до сих пор не потрудился коды программ выложить в интернет, чтобы не набирать их вручную.
Другая чрезвычайно интересная книга с точки зрения программирования математики [20]. Кодов программ в ней нет, зато есть текстовое описание и рисунки основных алгоритмов.
8. Ссылки
- JclMath. GitHub
- The GNU Multiple Precision Arithmetic Library
- Free Pascal interface for the GNU Multiple Precision Arithmetic Library in packages/gmp
- FreePascal и длинные числа. Часть 1. Библиотека GNU Multiple Precision Arithmetic (GMP)
- FFTW. Официальный сайт
- Graeme Geldenhuys - Interface unit for Fastest Fourier in the West library
- Matteo Frigo, Steven G. Johnson - FFTW
- Койнов Стас - Быстрое преобразование Фурье (реализация на языке Free Pascal)
- NumLib Documentation
- Библиотека численного анализа НИВЦ МГУ
- FORPAS - Конвертер программ с Фортрана на Паскаль
- Numerical Recipes. Home Page
- LMath на sourceforge.net
- Alglib is a cross-platform numerical analysis and data processing library
- Alglib. Страница скачивания
- Alglib. Документация для языка Delphi
- Welcome to Wolfgang Ehrhardt's home page!
- Turbo Pascal Developer Network. Математика
- Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. Томск: МП "РАСКО", 1991. - 272 с.
- Гловацкая А.П. Методы и алгоритмы вычислительной математики. Учеб. пособие для ВУЗов. - М.: Радио и связь, 1999. - 408 с.: ил.
Архивы библиотек:
- Архив Turbo Pascal Numerical Methods Toolbox
- Архив Numeric recipes for pascal
- Архив Numerical Methods. John Mathews
- Архив Compact Numerical Methods. Nash
- Архив LMath 0.4
Тесты:
- Исходники тестов скорости работы некоторых библиотек (решение СЛАУ)
| FPC | 3.2.2 | release |
| Lazarus | 3.2 | release |
| MSE | 5.10.0 | release |
| fpGUI | 1.4.1 | release |

