Подскажите алгоритм нахождения минимального расстояние от точки до кривой Безье(сплайна)? Для простоты сплайн 3 порядка на 4 точках.
Собственно отдельно интересно как это решено у zub в его редакторе.
Модератор: Модераторы
Как вариант, подойдёт этот (численный) алгоритм:

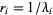
zub писал(а):В свое время интересовался этим, но так и не разобрался с математикой - забросил((. Мне для зкада нужна длина сплайна, ближайшая точка на сплайне и параметрическая точка на сплайне p(t) - это для базовой поддержки. Для резки\склейки соответственно неплохо иметь резку и склейку)) Буду рад любой помощи
interface
type
TDblPoint = packed record
x, y: double;
end;
PDblPoint = ^TDblPoint;
//расчёт точек для кривой Безье
//если количество точек aStep указано равным 0, либо оно меньше количества точек в aPoints
//то количество точек определяется из параметров массива aPoints
//первая и последняя точка включаются в состав точек и указанное количество
//то есть, если aStep = 5, то будет добавлено 3 точки внутри кривой, плюс первая и
//последняя опорные точки
procedure Bezie2Points(aP1, aP2, aP3: TPoint; var aPoints: array of TPoint; aStep: integer = 0); overload;
procedure Bezie2Points(aP1, aP2, aP3: TDblPoint; var aPoints: array of TDblPoint; aStep: integer = 0); overload;
procedure Bezie3Points(aP1, aP2, aP3, aP4: TPoint; var aPoints: array of TPoint; aStep: integer = 0); overload;
procedure Bezie3Points(aP1, aP2, aP3, aP4: TDblPoint; var aPoints: array of TDblPoint; aStep: integer = 0); overload;
implementation
procedure Bezie3Points(aP1, aP2, aP3, aP4: TPoint; var aPoints: array of TPoint; aStep: integer = 0);
const
MsInt = 4;
var
i, SegmCount: integer;
pl1, pl2, pl3, tp1, tp2, tp3, bp1, bp2: TPoint;
begin
SegmCount := Length(aPoints);
if (aStep = 0) or (aStep > SegmCount) then begin
aStep := SegmCount;
if aStep < 2 then exit;
end; // if
aStep -= 2;
SegmCount := aStep + 1;
aPoints[0].X := aP1.x;
aPoints[0].Y := aP1.Y;
if aStep < 1 then begin
aPoints[1].X := aP4.x;
aPoints[1].Y := aP4.Y;
Exit;
end; // if
aPoints[SegmCount].X := aP4.x;
aPoints[SegmCount].Y := aP4.Y;
aP1.x := aP1.x shl MsInt;
aP1.y := aP1.y shl MsInt;
aP2.x := aP2.x shl MsInt;
aP2.y := aP2.y shl MsInt;
aP3.x := aP3.x shl MsInt;
aP3.y := aP3.y shl MsInt;
aP4.x := aP4.x shl MsInt;
aP4.y := aP4.y shl MsInt;
pl1.x := aP2.x - aP1.x;
pl1.y := aP2.y - aP1.y;
pl2.x := aP3.x - aP2.x;
pl2.y := aP3.y - aP2.y;
pl3.x := aP4.x - aP3.x;
pl3.y := aP4.y - aP3.y;
for i := 1 to aStep do begin
tp1.x := aP1.x + ((pl1.x * i) div SegmCount);
tp1.y := aP1.y + ((pl1.y * i) div SegmCount);
tp2.x := aP2.x + ((pl2.x * i) div SegmCount);
tp2.y := aP2.y + ((pl2.y * i) div SegmCount);
tp3.x := aP3.x + ((pl3.x * i) div SegmCount);
tp3.y := aP3.y + ((pl3.y * i) div SegmCount);
bp1.x := tp1.x + (((tp2.x - tp1.x) * i) div SegmCount);
bp1.y := tp1.Y + (((tp2.y - tp1.y) * i) div SegmCount);
bp2.x := tp2.x + (((tp3.x - tp2.x) * i) div SegmCount);
bp2.y := tp2.Y + (((tp3.y - tp2.y) * i) div SegmCount);
aPoints[i].X := (bp1.x + (((bp2.x - bp1.x) * i) div SegmCount)) shr MsInt;
aPoints[i].Y := (bp1.Y + (((bp2.y - bp1.y) * i) div SegmCount)) shr MsInt;
end; // for
end;
procedure Bezie3Points(aP1, aP2, aP3, aP4: TDblPoint; var aPoints: array of TDblPoint; aStep: integer = 0);
var
i, SegmCount: integer;
pl1, pl2, pl3, tp1, tp2, tp3, bp1, bp2: TDblPoint;
begin
SegmCount := Length(aPoints);
if (aStep = 0) or (aStep > SegmCount) then begin
aStep := SegmCount;
if aStep < 2 then exit;
end;
aStep -= 2;
SegmCount := aStep + 1;
aPoints[0].X := aP1.x;
aPoints[0].Y := aP1.Y;
if aStep < 1 then begin
aPoints[1].X := aP4.x;
aPoints[1].Y := aP4.Y;
Exit;
end; // if
aPoints[SegmCount].X := aP4.x;
aPoints[SegmCount].Y := aP4.Y;
pl1.x := aP2.x - aP1.x;
pl1.y := aP2.y - aP1.y;
pl2.x := aP3.x - aP2.x;
pl2.y := aP3.y - aP2.y;
pl3.x := aP4.x - aP3.x;
pl3.y := aP4.y - aP3.y;
for i := 1 to aStep do begin
tp1.x := aP1.x + ((pl1.x * i) / SegmCount);
tp1.y := aP1.y + ((pl1.y * i) / SegmCount);
tp2.x := aP2.x + ((pl2.x * i) / SegmCount);
tp2.y := aP2.y + ((pl2.y * i) / SegmCount);
tp3.x := aP3.x + ((pl3.x * i) / SegmCount);
tp3.y := aP3.y + ((pl3.y * i) / SegmCount);
bp1.x := tp1.x + (((tp2.x - tp1.x) * i) / SegmCount);
bp1.y := tp1.Y + (((tp2.y - tp1.y) * i) / SegmCount);
bp2.x := tp2.x + (((tp3.x - tp2.x) * i) / SegmCount);
bp2.y := tp2.Y + (((tp3.y - tp2.y) * i) / SegmCount);
aPoints[i].X := bp1.x + (((bp2.x - bp1.x) * i) / SegmCount);
aPoints[i].Y := bp1.Y + (((bp2.y - bp1.y) * i) / SegmCount);
end; // for
end;
procedure Bezie2Points(aP1, aP2, aP3: TPoint; var aPoints: array of TPoint; aStep: integer = 0);
const
MsInt = 4;
var
i, SegmCount: integer;
pl1, pl2, tp1, tp2: TPoint;
begin
SegmCount := Length(aPoints);
if (aStep = 0) or (aStep > SegmCount) then begin
aStep := SegmCount;
if aStep < 2 then exit;
end; // if
aStep -= 2;
SegmCount := aStep + 1;
aPoints[0].X := aP1.x;
aPoints[0].Y := aP1.Y;
if aStep < 1 then begin
aPoints[1].X := aP3.x;
aPoints[1].Y := aP3.Y;
Exit;
end; // if
aPoints[SegmCount].X := aP3.x;
aPoints[SegmCount].Y := aP3.Y;
pl1.x := (aP2.x - aP1.x) shl MsInt;
pl1.y := (aP2.y - aP1.y) shl MsInt;
pl2.x := (aP3.x - aP2.x) shl MsInt;
pl2.y := (aP3.y - aP2.y) shl MsInt;
for i := 1 to aStep do begin
tp1.x := aP1.x + ((pl1.x * i) div SegmCount);
tp1.y := aP1.y + ((pl1.y * i) div SegmCount);
tp2.x := aP2.x + ((pl2.x * i) div SegmCount);
tp2.y := aP2.y + ((pl2.y * i) div SegmCount);
aPoints[i].X := (tp1.x + (((tp2.x - tp1.x) * i) div SegmCount)) shr MsInt;
aPoints[i].Y := (tp1.Y + (((tp2.y - tp1.y) * i) div SegmCount)) shr MsInt;
end; // for
end;
procedure Bezie2Points(aP1, aP2, aP3: TDblPoint; var aPoints: array of TDblPoint; aStep: integer = 0);
var
i, SegmCount: integer;
pl1, pl2, tp1, tp2: TDblPoint;
begin
SegmCount := Length(aPoints);
if (aStep = 0) or (aStep > SegmCount) then begin
aStep := SegmCount;
if aStep < 2 then exit;
end;
aStep -= 2;
SegmCount := aStep + 1;
aPoints[0].X := aP1.x;
aPoints[0].Y := aP1.Y;
if aStep < 1 then begin
aPoints[1].X := aP3.x;
aPoints[1].Y := aP3.Y;
Exit;
end; // if
aPoints[SegmCount].X := aP3.x;
aPoints[SegmCount].Y := aP3.Y;
pl1.x := aP2.x - aP1.x;
pl1.y := aP2.y - aP1.y;
pl2.x := aP3.x - aP2.x;
pl2.y := aP3.y - aP2.y;
for i := 1 to aStep do begin
tp1.x := aP1.x + ((pl1.x * i) / SegmCount);
tp1.y := aP1.y + ((pl1.y * i) / SegmCount);
tp2.x := aP2.x + ((pl2.x * i) / SegmCount);
tp2.y := aP2.y + ((pl2.y * i) / SegmCount);
aPoints[i].X := tp1.x + (((tp2.x - tp1.x) * i) / SegmCount);
aPoints[i].Y := tp1.Y + (((tp2.y - tp1.y) * i) / SegmCount);
end; // for
end;
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4