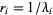freepascal.ru

Подскажите алгоритм нахождения минимального расстояние от точки до кривой Безье(сплайна)? Для простоты сплайн 3 порядка на 4 точках.

Собственно отдельно интересно как это решено у zub в его редакторе.

Обозначим четыре точки сплайна за p0=(x0,y0),p1=(x1,y1),p2=(x2,y2),p3=(x3,y3), а заданную точку за p=(x,y). Если 0<=t<=1 -- параметр спалйна, то вектор от заданной точки до точки t на сплайне задаётся формулой



Задача сводится к минимизации значения длины этого вектора. Вычислим длину вектора и сгруппируем их в многочлен по t, получится многочлен 6ой степени:



Ki вычисляются по некоторым простым (без ветвлений) формулам от изначальных точек. K6>0 всегда (если это действительно невырожденный кубический сплайн). Там, где многочлен достигает минимума, его производная равна нулю. Вычислим производную:



На этом вроде бы кончается точная часть, потому что (насколько я помню) общего хорошего алгоритма для нахождения всех действительных или всех комплексных корней произвольного многочлена ещё не придумано (но такой алгоритм, возможно, придуман для многочленов пятой степени).

Как вариант, подойдёт этот (численный) алгоритм:
https://habr.com/ru/post/303342/

Корни дадут от 1 до 5 кандидатов ближайшей точки на сплайне, плюс к ним нужно добавить точки t=0 и t=1, и остаётся просто перебором найти ту, на которой f(t) минимально.

Пора писать статью по методам оптимизации...

Как вариант, подойдёт этот (численный) алгоритм:

Таким смысла не у там дихотомия. Да и корни только действительные.
Я думаю взять алгоритм от сюда
http://mathworld.wolfram.com/PolynomialRoots.html


Правда не уверен что у них верное описание.

Я вот думаю для Безье известно что она почти точно представляется 16 линиями с шагом t=1/16 может так код быстрее будет?

В виде части "мозгового штурма"...
Почему нельзя просто прогнать все видимые точки сплайна на предмет расстояния до точки? Минимальное и будет искомым "расстоянием до сплайна" . Оптимизация методом постепенного приближения тоже понятна .

У меня сплайны поддерживаются "пока" только формально. В кавычках потому что нет ничего более постоянного чем чтото временное))
безье в зкаде нет, есть нурбс. Но он только рисуется (с помощью glu) и редактируется по контролным точкам, привязок на него и операций типа разрезать - нет
В свое время интересовался этим, но так и не разобрался с математикой - забросил((. Мне для зкада нужна длина сплайна, ближайшая точка на сплайне и параметрическая точка на сплайне p(t) - это для базовой поддержки. Для резки\склейки соответственно неплохо иметь резку и склейку)) Буду рад любой помощи

лучше искать по английски, "spline Near point"
https://borjaportugal.com/2018/01/13/fi ... to-spline/

zub писал(а):В свое время интересовался этим, но так и не разобрался с математикой - забросил((. Мне для зкада нужна длина сплайна, ближайшая точка на сплайне и параметрическая точка на сплайне p(t) - это для базовой поддержки. Для резки\склейки соответственно неплохо иметь резку и склейку)) Буду рад любой помощи

Точка считается по формуле P = At^3 + Bt^2 + Ct + D.
Ближайшая точка брутфорсом проще всего. Думаю достаточно будет.
Длина им же.
Резка/склейка специальным алгоритмом. Довольно простым насколько помню, по крайней мере для безье.

Держите готовые проверенные функции для вычисления точек кривой Безье с заданным количеством шагов для 2 и 3 порядка.

Код: Выделить всё

interface

type

  TDblPoint = packed record
    x, y: double;
  end;
  PDblPoint = ^TDblPoint;

//расчёт точек для кривой Безье
//если количество точек aStep указано равным 0, либо оно меньше количества точек в aPoints
//то количество точек определяется из параметров массива aPoints
//первая и последняя точка включаются в состав точек и указанное количество
//то есть, если aStep = 5, то будет добавлено 3 точки внутри кривой, плюс первая и
//последняя опорные точки
procedure Bezie2Points(aP1, aP2, aP3: TPoint; var aPoints: array of TPoint; aStep: integer = 0); overload;
procedure Bezie2Points(aP1, aP2, aP3: TDblPoint; var aPoints: array of TDblPoint; aStep: integer = 0); overload;

procedure Bezie3Points(aP1, aP2, aP3, aP4: TPoint; var aPoints: array of TPoint; aStep: integer = 0); overload;
procedure Bezie3Points(aP1, aP2, aP3, aP4: TDblPoint; var aPoints: array of TDblPoint; aStep: integer = 0); overload;

implementation

procedure Bezie3Points(aP1, aP2, aP3, aP4: TPoint; var aPoints: array of TPoint; aStep: integer = 0);
const
  MsInt = 4;
var
  i, SegmCount: integer;
  pl1, pl2, pl3, tp1, tp2, tp3, bp1, bp2: TPoint;
begin
  SegmCount := Length(aPoints);
  if (aStep = 0) or (aStep > SegmCount) then begin
    aStep := SegmCount;
    if aStep < 2 then exit;
  end; // if

  aStep -= 2;
  SegmCount := aStep + 1;

  aPoints[0].X := aP1.x;
  aPoints[0].Y := aP1.Y;

  if aStep < 1 then begin
    aPoints[1].X := aP4.x;
    aPoints[1].Y := aP4.Y;
    Exit;
  end; // if
  aPoints[SegmCount].X := aP4.x;
  aPoints[SegmCount].Y := aP4.Y;

  aP1.x := aP1.x shl MsInt;
  aP1.y := aP1.y shl MsInt;
  aP2.x := aP2.x shl MsInt;
  aP2.y := aP2.y shl MsInt;
  aP3.x := aP3.x shl MsInt;
  aP3.y := aP3.y shl MsInt;
  aP4.x := aP4.x shl MsInt;
  aP4.y := aP4.y shl MsInt;

  pl1.x := aP2.x - aP1.x;
  pl1.y := aP2.y - aP1.y;

  pl2.x := aP3.x - aP2.x;
  pl2.y := aP3.y - aP2.y;

  pl3.x := aP4.x - aP3.x;
  pl3.y := aP4.y - aP3.y;

  for i := 1 to aStep do begin
    tp1.x := aP1.x + ((pl1.x * i) div SegmCount);
    tp1.y := aP1.y + ((pl1.y * i) div SegmCount);
    tp2.x := aP2.x + ((pl2.x * i) div SegmCount);
    tp2.y := aP2.y + ((pl2.y * i) div SegmCount);
    tp3.x := aP3.x + ((pl3.x * i) div SegmCount);
    tp3.y := aP3.y + ((pl3.y * i) div SegmCount);

    bp1.x := tp1.x + (((tp2.x - tp1.x) * i) div SegmCount);
    bp1.y := tp1.Y + (((tp2.y - tp1.y) * i) div SegmCount);
    bp2.x := tp2.x + (((tp3.x - tp2.x) * i) div SegmCount);
    bp2.y := tp2.Y + (((tp3.y - tp2.y) * i) div SegmCount);


    aPoints[i].X := (bp1.x + (((bp2.x - bp1.x) * i) div SegmCount)) shr MsInt;
    aPoints[i].Y := (bp1.Y + (((bp2.y - bp1.y) * i) div SegmCount)) shr MsInt;
  end; // for
end;

procedure Bezie3Points(aP1, aP2, aP3, aP4: TDblPoint; var aPoints: array of TDblPoint; aStep: integer = 0);
var
  i, SegmCount: integer;
  pl1, pl2, pl3, tp1, tp2, tp3, bp1, bp2: TDblPoint;
begin
  SegmCount := Length(aPoints);
  if (aStep = 0) or (aStep > SegmCount) then begin
    aStep := SegmCount;
    if aStep < 2 then exit;
  end;

  aStep -= 2;
  SegmCount := aStep + 1;

  aPoints[0].X := aP1.x;
  aPoints[0].Y := aP1.Y;

  if aStep < 1 then begin
    aPoints[1].X := aP4.x;
    aPoints[1].Y := aP4.Y;
    Exit;
  end; // if
  aPoints[SegmCount].X := aP4.x;
  aPoints[SegmCount].Y := aP4.Y;

  pl1.x := aP2.x - aP1.x;
  pl1.y := aP2.y - aP1.y;

  pl2.x := aP3.x - aP2.x;
  pl2.y := aP3.y - aP2.y;

  pl3.x := aP4.x - aP3.x;
  pl3.y := aP4.y - aP3.y;

  for i := 1 to aStep do begin
    tp1.x := aP1.x + ((pl1.x * i) / SegmCount);
    tp1.y := aP1.y + ((pl1.y * i) / SegmCount);
    tp2.x := aP2.x + ((pl2.x * i) / SegmCount);
    tp2.y := aP2.y + ((pl2.y * i) / SegmCount);
    tp3.x := aP3.x + ((pl3.x * i) / SegmCount);
    tp3.y := aP3.y + ((pl3.y * i) / SegmCount);

    bp1.x := tp1.x + (((tp2.x - tp1.x) * i) / SegmCount);
    bp1.y := tp1.Y + (((tp2.y - tp1.y) * i) / SegmCount);
    bp2.x := tp2.x + (((tp3.x - tp2.x) * i) / SegmCount);
    bp2.y := tp2.Y + (((tp3.y - tp2.y) * i) / SegmCount);


    aPoints[i].X := bp1.x + (((bp2.x - bp1.x) * i) / SegmCount);
    aPoints[i].Y := bp1.Y + (((bp2.y - bp1.y) * i) / SegmCount);
  end; // for
end;

procedure Bezie2Points(aP1, aP2, aP3: TPoint; var aPoints: array of TPoint; aStep: integer = 0);
const
  MsInt = 4;
var
  i, SegmCount: integer;
  pl1, pl2, tp1, tp2: TPoint;
begin
  SegmCount := Length(aPoints);
  if (aStep = 0) or (aStep > SegmCount) then begin
    aStep := SegmCount;
    if aStep < 2 then exit;
  end; // if

  aStep -= 2;
  SegmCount := aStep + 1;

  aPoints[0].X := aP1.x;
  aPoints[0].Y := aP1.Y;

  if aStep < 1 then begin
    aPoints[1].X := aP3.x;
    aPoints[1].Y := aP3.Y;
    Exit;
  end; // if
  aPoints[SegmCount].X := aP3.x;
  aPoints[SegmCount].Y := aP3.Y;

  pl1.x := (aP2.x - aP1.x) shl MsInt;
  pl1.y := (aP2.y - aP1.y) shl MsInt;

  pl2.x := (aP3.x - aP2.x) shl MsInt;
  pl2.y := (aP3.y - aP2.y) shl MsInt;

  for i := 1 to aStep do begin
    tp1.x := aP1.x + ((pl1.x * i) div SegmCount);
    tp1.y := aP1.y + ((pl1.y * i) div SegmCount);
    tp2.x := aP2.x + ((pl2.x * i) div SegmCount);
    tp2.y := aP2.y + ((pl2.y * i) div SegmCount);

    aPoints[i].X := (tp1.x + (((tp2.x - tp1.x) * i) div SegmCount)) shr MsInt;
    aPoints[i].Y := (tp1.Y + (((tp2.y - tp1.y) * i) div SegmCount)) shr MsInt;
  end; // for
end;

procedure Bezie2Points(aP1, aP2, aP3: TDblPoint; var aPoints: array of TDblPoint; aStep: integer = 0);
var
  i, SegmCount: integer;
  pl1, pl2, tp1, tp2: TDblPoint;
begin
  SegmCount := Length(aPoints);
  if (aStep = 0) or (aStep > SegmCount) then begin
    aStep := SegmCount;
    if aStep < 2 then exit;
  end;

  aStep -= 2;
  SegmCount := aStep + 1;

  aPoints[0].X := aP1.x;
  aPoints[0].Y := aP1.Y;

  if aStep < 1 then begin
    aPoints[1].X := aP3.x;
    aPoints[1].Y := aP3.Y;
    Exit;
  end; // if
  aPoints[SegmCount].X := aP3.x;
  aPoints[SegmCount].Y := aP3.Y;

  pl1.x := aP2.x - aP1.x;
  pl1.y := aP2.y - aP1.y;

  pl2.x := aP3.x - aP2.x;
  pl2.y := aP3.y - aP2.y;

  for i := 1 to aStep do begin
    tp1.x := aP1.x + ((pl1.x * i) / SegmCount);
    tp1.y := aP1.y + ((pl1.y * i) / SegmCount);
    tp2.x := aP2.x + ((pl2.x * i) / SegmCount);
    tp2.y := aP2.y + ((pl2.y * i) / SegmCount);

    aPoints[i].X := tp1.x + (((tp2.x - tp1.x) * i) / SegmCount);
    aPoints[i].Y := tp1.Y + (((tp2.y - tp1.y) * i) / SegmCount);
  end; // for
end;


Для целочисленного варианта используется масштабирование на 4 разряда, чтобы не терялась точность вычислений, иначе видны косяки округления при делении.

Дальше всё сводится к задаче определения минимального расстояния до набора отрезков. Само собой, что чем больше сегментов, тем точнее рузельтат.

Zub'у для ЗКада тоже может пригодиться. Дарю!