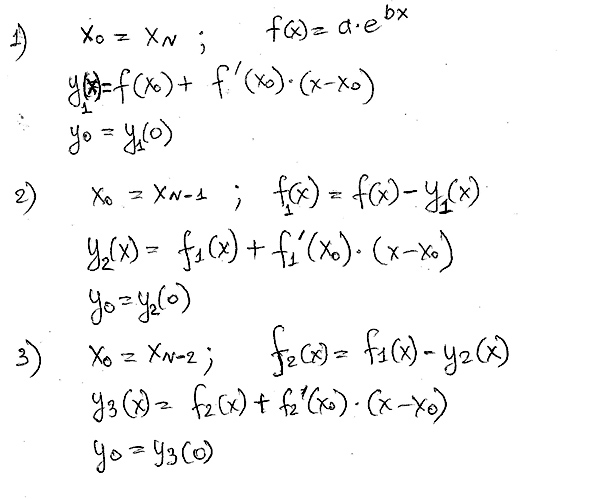Действия над функциями
Столкнулся с такой проблемой: надо запрограммировать действия над несколькими функциями.
Пробовал делать через передачу параметрова переменнй типа функции, но не получилось.
Сам алгоритм такой: есть некоторая функция y1(x). Далее записываем уравнение касательной y1(x) к ней в точке x0=x[n],
далее получаем функцию y2(x) как разность y1(x) и yk1(x) и получаем уравнение касательной в точке x0=x[n-1] и т.д.
по всем точкам из массива x.
Итерация 1
x0=x[n]
y1(x)=a*exp(b*x)
yk1(x)=y1(x0)+(dy1(x0)/dx)*(x-x0)
y0=yk1(0)
Итерация 1
x0=x[n-1]
y2(x)=y1(x)-yk1(x)
yk2(x)=y2(x0)+(dy2(x0)/dx)*(x-x0)
y0=yk2(0)
Итерация 1
x0=x[n-2]
y3(x)=y2(x)-yk2(x)
.................
dy1(x0)/dx - значение производной функции y1(x) в точке x0
Пробовал делать через передачу параметрова переменнй типа функции, но не получилось.
Сам алгоритм такой: есть некоторая функция y1(x). Далее записываем уравнение касательной y1(x) к ней в точке x0=x[n],
далее получаем функцию y2(x) как разность y1(x) и yk1(x) и получаем уравнение касательной в точке x0=x[n-1] и т.д.
по всем точкам из массива x.
Итерация 1
x0=x[n]
y1(x)=a*exp(b*x)
yk1(x)=y1(x0)+(dy1(x0)/dx)*(x-x0)
y0=yk1(0)
Итерация 1
x0=x[n-1]
y2(x)=y1(x)-yk1(x)
yk2(x)=y2(x0)+(dy2(x0)/dx)*(x-x0)
y0=yk2(0)
Итерация 1
x0=x[n-2]
y3(x)=y2(x)-yk2(x)
.................
dy1(x0)/dx - значение производной функции y1(x) в точке x0